Question

如图以O为圆心的两个同心圆，AB经过圆心O，且与小圆相交于点A，与大圆相交于点B，小圆的切线AC与大圆相交于点D，且OC平分∠ACB．

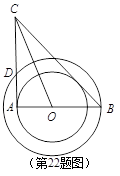
1.试判断BC所在的直线与小圆的位置关系，并说明理由

2.试判断线段AC、AD、BC之间的数量关系，并说明理由

3.若AB＝8cm，BC＝10cm，求大圆与小圆围成的圆环的面积（结果保留π）．

 

Answer 1

 

1.相切，过O作OE⊥BC交BC交E得用角平分线性质证OE＝OA

2.BC＝AC＋AD，连OD证△AOD≌△EOB

3.可得AC＝6，由⑵得BE＝4，S_环形面积＝π(OB²－OE²)＝16π

 解析:略