题目内容
【题目】定义:在平面直角坐标系中,对于任意两点A (a,b),B(c,d),若点T(x,y)满足x=![]() ,y=
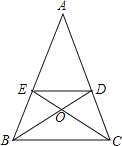
,y=![]() ,那么称点T是点A和B的融合点.例如:M(﹣1,8),N(4,﹣2),则点T(1,2)是点M和N的融合点.如图,已知点D(3,0),点E是直线y=x+2上任意一点,点T (x,y)是点D和E的融合点.
,那么称点T是点A和B的融合点.例如:M(﹣1,8),N(4,﹣2),则点T(1,2)是点M和N的融合点.如图,已知点D(3,0),点E是直线y=x+2上任意一点,点T (x,y)是点D和E的融合点.
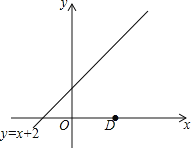
(1)若点E的纵坐标是6,则点T的坐标为 ;
(2)求点T (x,y)的纵坐标y与横坐标x的函数关系式:
(3)若直线ET交x轴于点H,当△DTH为直角三角形时,求点E的坐标.
【答案】(1)(![]() ,2);(2)y=x﹣
,2);(2)y=x﹣![]() ;(3)E的坐标为(
;(3)E的坐标为(![]() ,
,![]() )或(6,8)
)或(6,8)
【解析】
(1)把点E的纵坐标代入直线解析式,求出横坐标,得到点E的坐标,根据融合点的定义求求解即可;
(2)设点E的坐标为(a,a+2),根据融合点的定义用a表示出x、y,整理得到答案;
(3)分∠THD=90°、∠TDH=90°、∠DTH=90°三种情况,根据融合点的定义解答.
解:(1)∵点E是直线y=x+2上一点,点E的纵坐标是6,
∴x+2=6,
解得,x=4,
∴点E的坐标是(4,6),
∵点T (x,y)是点D和E的融合点,
∴x=![]() =
=![]() ,y=
,y=![]() =2,
=2,
∴点T的坐标为(![]() ,2),
,2),
故答案为:(![]() ,2);
,2);
(2)设点E的坐标为(a,a+2),
∵点T (x,y)是点D和E的融合点,
∴x=![]() ,y=
,y=![]() ,
,
解得,a=3x﹣3,a=3y﹣2,
∴3x﹣3=3y﹣2,
整理得,y=x﹣![]() ;
;
(3)设点E的坐标为(a,a+2),
则点T的坐标为(![]() ,
,![]() ),
),
当∠THD=90°时,点E与点T的横坐标相同,
∴![]() =a,
=a,
解得,a=![]() ,
,
此时点E的坐标为(![]() ,
,![]() ),
),
当∠TDH=90°时,点T与点D的横坐标相同,
∴![]() =3,
=3,
解得,a=6,
此时点E的坐标为(6,8),
当∠DTH=90°时,该情况不存在,
综上所述,当△DTH为直角三角形时,点E的坐标为(![]() ,
,![]() )或(6,8)
)或(6,8)

【题目】某中学八⑴班、⑵班各选5名同学参加“爱我中华”演讲比赛,其预赛成绩(满分100分)如图所示:
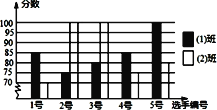
(1)根据上图填写下表:
平均数 | 中位数 | 众数 | |
八(1)班 | 85 | 85 | |
八(2)班 | 85 | 80 |
(2)根据两班成绩的平均数和中位数,分析哪班成绩较好?
(3)如果每班各选2名同学参加决赛,你认为哪个班实力更强些?请说明理由.