题目内容
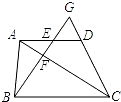 题甲:如图,梯形ABCD中,AD∥BC,点E是边AD的中点,连接BE交AC于点F,BE的延长线交CD的延长线于点G.
题甲:如图,梯形ABCD中,AD∥BC,点E是边AD的中点,连接BE交AC于点F,BE的延长线交CD的延长线于点G.
(1)求证: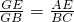 ;
;
(2)若GE=2,BF=3,求线段EF的长.
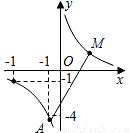
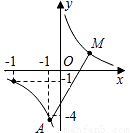
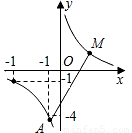
题乙:如图,反比例函数y= 的图象,当-4≤x≤-1时,-4≤y≤-1.
的图象,当-4≤x≤-1时,-4≤y≤-1.
(1)求该反比例函数的解析式;
(2)若M,N分别在反比例函数图象的两支上,请指出什么情况下线段MN最短(不需证明),并求出线段MN长度的取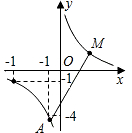 值范围.
值范围.
甲题:
(1)证明:∵AD∥BC
∴△GED∽△GBC
∴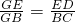
又∵点E是边AD的中点
∴AE=ED
∴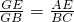
(2)解:∵AD∥BC
∴△AEF∽△CBF
∴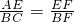
由(1)知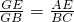
∴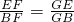
设EF=x,则GB=5+x,
则有
即x2+5x-6=0
解得:x=1或x=-6,
经检验,x=1或x=-6都是原方程的根,但x=-6不合题意,舍去.
故EF的长为1.
乙题:
解:(1)因为反比例函数的图象经过点(-1,-4)
有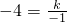
∴k=4
所以反比例函数的解析式为 .
.
(2)当M,N为-,三象限角平分线与反比例函数图象的交点时,线段MN最短.
将y=x代入 ,
,
解得
 ,
,
即M(2,2),N(-2,-2).
∴OM=2 .
.
则MN=4 .
.
又∵M,N为反比例函数图象上的任意两点,
由图象特点知,线段MN无最大值,即MN≥4 .
.
分析:甲:(1)因为AD∥BC,所以△GED∽△GBC,所以两三角形的对应边成比例;又点E是边AD的中点,AE=ED.此题得证
(2)AD∥BC还可以得到△AEF∽△CBF,又AE=ED,通过等量代换即可得到GE、GB、EF、FB之间的关系.
乙:(1)图象经过A(-1,-4),可用待定系数法求解.
(2)考虑经过原点并且在同一直线上,也就成了线段MN.
点评:题甲:主要考查相似三角形对应边成比例,点E是边AD的中点得AE=ED是突破口
题乙:主要考查待定系数法求反比例函数解析式,猜想时首选经过原点.
(1)证明:∵AD∥BC
∴△GED∽△GBC
∴
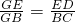
又∵点E是边AD的中点
∴AE=ED
∴
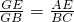
(2)解:∵AD∥BC
∴△AEF∽△CBF
∴
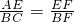
由(1)知
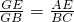
∴
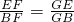
设EF=x,则GB=5+x,
则有

即x2+5x-6=0
解得:x=1或x=-6,
经检验,x=1或x=-6都是原方程的根,但x=-6不合题意,舍去.
故EF的长为1.
乙题:
解:(1)因为反比例函数的图象经过点(-1,-4)
有
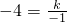
∴k=4
所以反比例函数的解析式为
 .
.(2)当M,N为-,三象限角平分线与反比例函数图象的交点时,线段MN最短.
将y=x代入
 ,
,解得

 ,
,即M(2,2),N(-2,-2).
∴OM=2
 .
.则MN=4
 .
.又∵M,N为反比例函数图象上的任意两点,
由图象特点知,线段MN无最大值,即MN≥4
 .
.分析:甲:(1)因为AD∥BC,所以△GED∽△GBC,所以两三角形的对应边成比例;又点E是边AD的中点,AE=ED.此题得证
(2)AD∥BC还可以得到△AEF∽△CBF,又AE=ED,通过等量代换即可得到GE、GB、EF、FB之间的关系.
乙:(1)图象经过A(-1,-4),可用待定系数法求解.
(2)考虑经过原点并且在同一直线上,也就成了线段MN.
点评:题甲:主要考查相似三角形对应边成比例,点E是边AD的中点得AE=ED是突破口
题乙:主要考查待定系数法求反比例函数解析式,猜想时首选经过原点.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
 从甲,乙两题中选做一题,如果两题都做,只以甲题计分.
从甲,乙两题中选做一题,如果两题都做,只以甲题计分. 值范围.
值范围.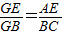 ;
;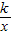 的图象,当-4≤x≤-1时,-4≤y≤-1.
的图象,当-4≤x≤-1时,-4≤y≤-1.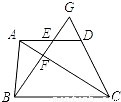
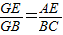 ;
;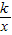 的图象,当-4≤x≤-1时,-4≤y≤-1.
的图象,当-4≤x≤-1时,-4≤y≤-1.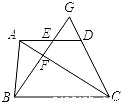
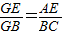 ;
;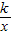 的图象,当-4≤x≤-1时,-4≤y≤-1.
的图象,当-4≤x≤-1时,-4≤y≤-1.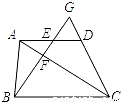
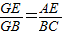 ;
;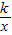 的图象,当-4≤x≤-1时,-4≤y≤-1.
的图象,当-4≤x≤-1时,-4≤y≤-1.
