题目内容
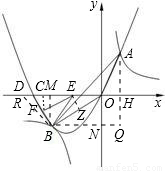
如图,二次函数y=ax2+bx(a>0)的图象与反比例函数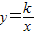 图象相交于点A,B,已知点A的坐标为(1,4),点B在第三象限内,且△AOB的面积为3(O为坐标原点).
图象相交于点A,B,已知点A的坐标为(1,4),点B在第三象限内,且△AOB的面积为3(O为坐标原点).①求实数k的值;
②求二次函数y=ax2+bx(a>0)的解析式;
③设抛物线与x轴的另一个交点为D,E点为线段OD上的动点(与O,D不能重合),过E点作EF∥OB交BD于F,连接BE,设OE的长为m,△BEF的面积为S,求S于m的函数关系式;
④在③的基础上,试说明S是否存在最大值?若存在,请求出S的最大值,并求出此时E点的坐标;若不存在,说明理由.
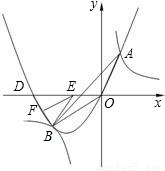
【答案】分析:①把A(1,4)代入即可;
②过B作BM⊥x轴于M,BN⊥y轴于N,过A作AH⊥x轴于H,两线BN和AH交于Q,设OM=c,ON=d,c>0,d>o,根据S=S△ABQ-S△AOH-S△BNO-S矩形ONQH,和cd=4,求出c=2,d=2,得到B(-2,-2),把A(1,4)和B(-2,-2)代入抛物线得出方程组 ,求出方程组得解即可;
,求出方程组得解即可;
③充分利用(-2,-2)这一坐标,由△DFE相似于△DBO求得EF的长(含m),再表示出F到x轴的距离,利用△EDB的面积减去△EDF的面积即可建立S与m的函数关系
④S= m(1+
m(1+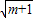 -m),当m=
-m),当m= 时,S最大,把m=
时,S最大,把m= 代入即可求出s,从而得到E的坐标.
代入即可求出s,从而得到E的坐标.
解答:解:①把A(1,4)代入得:k=xy=4,
答:实数k的值是4.
②过B作BM⊥x轴于M,BN⊥y轴于N,过A作AH⊥x轴于H,两线BN和AH交于Q,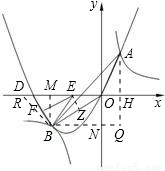
设OM=c,ON=d,c>0,d>o,
则:S=S△ABQ-S△AOH-S△BNO-S矩形ONQH,
即:3= (1+c)(4+d)-
(1+c)(4+d)- ×1×4-
×1×4- cd-d×1,
cd-d×1,
cd=k=4,
解得:c=2,d=2,
∴B(-2,-2),
把A(1,4)和B(-2,-2)代入抛物线得: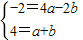 ,
,
解得: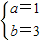 ,
,
∴y=x2+3x,
答:二次函数y=ax2+bx(a>0)的解析式是y=x2+3x.
⑨把y=0代入y=x2+3x得:x2+3x=0,
解得:x1=0,x2=-3,
∴D(-3,0),
即OD=3,
∵B(-2,-2),
∴由勾股定理得:OB=2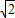 ,
,
∵EF∥OB,
∴△DFE∽△DBO,
∴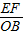 =
=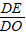 ,
,
∴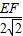 =
=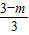 ,
,
∴EF=2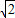 -
-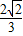 m,
m,
过F作FC⊥x轴于C,
根据相似三角形的对应高之比等于相似比得: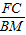 =
=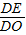 ,
,
∴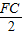 =
= ,
,
FC=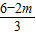
S=S△EDB-S△EDF
= DE×BM-
DE×BM- FC×DE,
FC×DE,
即S=- m2+m,
m2+m,
∴S与m的函数关系S=- m2+m.
m2+m.
④S=- m2+m.
m2+m.
当m= 时,S最大,是
时,S最大,是 ,
,
∴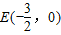 ,
,
答:在③的基础上,S存在最大值,S的最大值是 ,此时E点的坐标是(-
,此时E点的坐标是(- ,0).
,0).
点评:本题主要考查对用待定系数法求二次函数的解析式,反比例函数的图象上点的坐标特征,解二元一次方程,三角形的面积,平行线的性质,勾股定理,函数的最值,锐角三角函数的定义等知识点的理解和掌握,能熟练地运用这些性质进行计算是解此题的关键,此题是一个拔高的题目,有一定的难度.
②过B作BM⊥x轴于M,BN⊥y轴于N,过A作AH⊥x轴于H,两线BN和AH交于Q,设OM=c,ON=d,c>0,d>o,根据S=S△ABQ-S△AOH-S△BNO-S矩形ONQH,和cd=4,求出c=2,d=2,得到B(-2,-2),把A(1,4)和B(-2,-2)代入抛物线得出方程组
 ,求出方程组得解即可;
,求出方程组得解即可;③充分利用(-2,-2)这一坐标,由△DFE相似于△DBO求得EF的长(含m),再表示出F到x轴的距离,利用△EDB的面积减去△EDF的面积即可建立S与m的函数关系
④S=
 m(1+
m(1+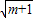 -m),当m=
-m),当m= 时,S最大,把m=
时,S最大,把m= 代入即可求出s,从而得到E的坐标.
代入即可求出s,从而得到E的坐标.解答:解:①把A(1,4)代入得:k=xy=4,
答:实数k的值是4.
②过B作BM⊥x轴于M,BN⊥y轴于N,过A作AH⊥x轴于H,两线BN和AH交于Q,

设OM=c,ON=d,c>0,d>o,
则:S=S△ABQ-S△AOH-S△BNO-S矩形ONQH,
即:3=
 (1+c)(4+d)-
(1+c)(4+d)- ×1×4-
×1×4- cd-d×1,
cd-d×1,cd=k=4,
解得:c=2,d=2,
∴B(-2,-2),
把A(1,4)和B(-2,-2)代入抛物线得:
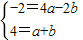 ,
,解得:
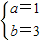 ,
,∴y=x2+3x,
答:二次函数y=ax2+bx(a>0)的解析式是y=x2+3x.
⑨把y=0代入y=x2+3x得:x2+3x=0,
解得:x1=0,x2=-3,
∴D(-3,0),
即OD=3,
∵B(-2,-2),
∴由勾股定理得:OB=2
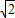 ,
,∵EF∥OB,
∴△DFE∽△DBO,
∴
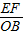 =
=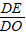 ,
,∴
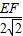 =
=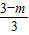 ,
,∴EF=2
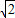 -
-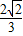 m,
m,过F作FC⊥x轴于C,
根据相似三角形的对应高之比等于相似比得:
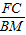 =
=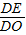 ,
,∴
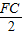 =
= ,
,FC=
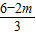

S=S△EDB-S△EDF
=
 DE×BM-
DE×BM- FC×DE,
FC×DE,即S=-
 m2+m,
m2+m,∴S与m的函数关系S=-
 m2+m.
m2+m.④S=-
 m2+m.
m2+m.当m=
 时,S最大,是
时,S最大,是 ,
,∴
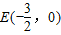 ,
,答:在③的基础上,S存在最大值,S的最大值是
 ,此时E点的坐标是(-
,此时E点的坐标是(- ,0).
,0).点评:本题主要考查对用待定系数法求二次函数的解析式,反比例函数的图象上点的坐标特征,解二元一次方程,三角形的面积,平行线的性质,勾股定理,函数的最值,锐角三角函数的定义等知识点的理解和掌握,能熟练地运用这些性质进行计算是解此题的关键,此题是一个拔高的题目,有一定的难度.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
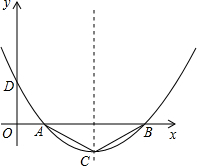 如图,二次函数的图象经过点D(0,
如图,二次函数的图象经过点D(0,
 如图,二次函数y=ax2+bx+c的图象与x轴交于B、C两点,与y轴交于点A(0,-3),∠ABC=45°,∠ACB=60°,求这个二次函数解析式.
如图,二次函数y=ax2+bx+c的图象与x轴交于B、C两点,与y轴交于点A(0,-3),∠ABC=45°,∠ACB=60°,求这个二次函数解析式. 某公司推出了一种高效环保型洗涤用品,年初上市后,公司经历了从亏损到盈利的过程,如图的二次函数图象(部分)刻画了该公司年初以来累积利润s(万元)与时间t(月)之间的关系(即前t个月的利润总和s与t之间的关系).根据图象提供的信息,解答下列问题:
某公司推出了一种高效环保型洗涤用品,年初上市后,公司经历了从亏损到盈利的过程,如图的二次函数图象(部分)刻画了该公司年初以来累积利润s(万元)与时间t(月)之间的关系(即前t个月的利润总和s与t之间的关系).根据图象提供的信息,解答下列问题: 如图,二次函数y=ax2+bx+c的图象与x轴相交于两个点,根据图象回答:(1)b
如图,二次函数y=ax2+bx+c的图象与x轴相交于两个点,根据图象回答:(1)b