题目内容
化简:|2x+1|-|x-3|+|x-6|
解:∵由2x+1=0、x-3=0、x-6=0分别求得:x=- ,x=3,x=6,
,x=3,x=6,
当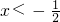 时,原式=-(2x+1)+(x-3)-(x-6)=-2x+2;
时,原式=-(2x+1)+(x-3)-(x-6)=-2x+2;
当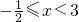 时,原式=(2x+1)+(x-3)-(x-6)=2x+4;
时,原式=(2x+1)+(x-3)-(x-6)=2x+4;
当3≤x<6时,原式=(2x+1)-(x-3)-(x-6)=10;
当x≥6时,原式=(2x+1)-(x-3)+(x-6)=2x-2;
∴原式= .
.
分析:先分别令2x+1=0、x-3=0、x-6=0分别求出x的对应值,再根据x的取值范围利用绝对值的性质去掉绝对值符号即可.
点评:本题考查的是绝对值的性质,在解答此题时要注意应用分类讨论的思想,不要漏解.
 ,x=3,x=6,
,x=3,x=6,当
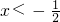 时,原式=-(2x+1)+(x-3)-(x-6)=-2x+2;
时,原式=-(2x+1)+(x-3)-(x-6)=-2x+2;当
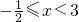 时,原式=(2x+1)+(x-3)-(x-6)=2x+4;
时,原式=(2x+1)+(x-3)-(x-6)=2x+4;当3≤x<6时,原式=(2x+1)-(x-3)-(x-6)=10;
当x≥6时,原式=(2x+1)-(x-3)+(x-6)=2x-2;
∴原式=
 .
.分析:先分别令2x+1=0、x-3=0、x-6=0分别求出x的对应值,再根据x的取值范围利用绝对值的性质去掉绝对值符号即可.
点评:本题考查的是绝对值的性质,在解答此题时要注意应用分类讨论的思想,不要漏解.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目