题目内容
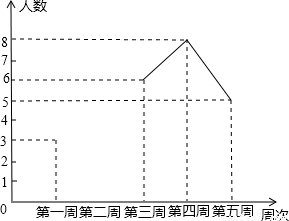
为配合学校开展的“书香校园读书日”活动,我校初二某班的社会实践活动小组就该班同学近五周的读书情况进行了调查,将当周每日都坚持课外阅读的同学评为“读书之星”并将“读书之星”的人数与周次制成了如下不完整的折线统计图:(1)已知这五周“读书之星”人数的众数为8人,求该班这五周“读书之星”人数的平均数;
(2)将折线统计图补充完整;
(3)若第五周的“读书之星”同学中,同学A和B一直坚持得比较好,现在该社会实践活动小组将从第五周的“读书之星”中,随机抽出两位同学谈谈他们的收获,请你用列表或画树状图的方法,求出所选两位同学恰好是同学A和B的概率.
【答案】分析:(1)根据众数的定义可得第二周每日都坚持读书的有8人,再根据算术平均数的计算方法进行计算即可得解;
(2)根据第二周每日都坚持读书的有8人补全统计图即可;
(3)设同学分别为A、B、C、D、E,用列表法列出所有可能情况,然后根据概率的定义解答.
解答:解(1)∵众数为8,
∴第二周每日都坚持读书的有8人,
∴其平均人数为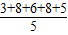 =6;
=6;
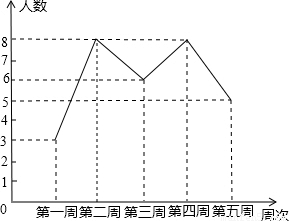
(2)补全统计图如图所示;
(3)设同学分别为A、B、C、D、E,
列表如下:
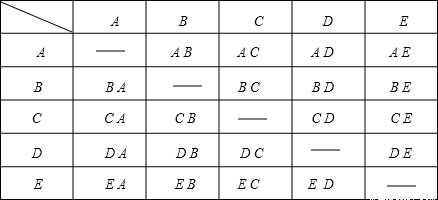
由图可知,总的情况数为20种,恰好是同学A和B的有2种,
所以P(A和B)=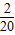 =
=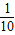 .
.
点评:本题考查了折线统计图的综合运用,列表法与树状图法,折线统计图表示的是事物的变化情况,根据众数的定义得出第二周每日都坚持读书的有8人是解题的关键.
(2)根据第二周每日都坚持读书的有8人补全统计图即可;
(3)设同学分别为A、B、C、D、E,用列表法列出所有可能情况,然后根据概率的定义解答.
解答:解(1)∵众数为8,
∴第二周每日都坚持读书的有8人,
∴其平均人数为
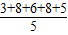 =6;
=6;(2)补全统计图如图所示;

(3)设同学分别为A、B、C、D、E,
列表如下:

由图可知,总的情况数为20种,恰好是同学A和B的有2种,
所以P(A和B)=
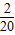 =
=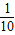 .
.点评:本题考查了折线统计图的综合运用,列表法与树状图法,折线统计图表示的是事物的变化情况,根据众数的定义得出第二周每日都坚持读书的有8人是解题的关键.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目
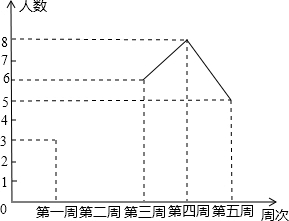 坚持课外阅读的同学评为“读书之星”并将“读书之星”的人数与周次制成了如下不完整的折线统计图:
坚持课外阅读的同学评为“读书之星”并将“读书之星”的人数与周次制成了如下不完整的折线统计图: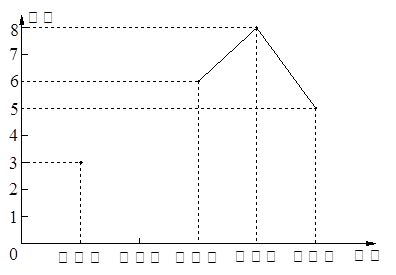
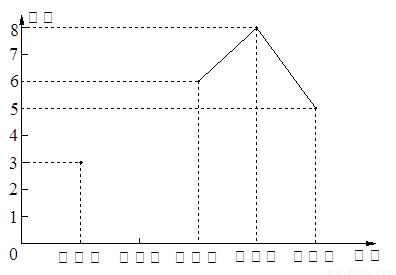
 坚持课外阅读的同学评为“读书之星”并将“读书之星”的人数与周次制成了如下不完整的折线统计图:
坚持课外阅读的同学评为“读书之星”并将“读书之星”的人数与周次制成了如下不完整的折线统计图: