题目内容
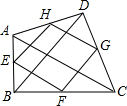 如图,已知四边形ABCD中,AC=BD,E、F、G、H分别是AB、BC、CD、DA边上的中点.
如图,已知四边形ABCD中,AC=BD,E、F、G、H分别是AB、BC、CD、DA边上的中点.求证:四边形EFGH是菱形.
分析:根据三角形的中位线定理和菱形的判定,可得顺次连接对角线相等的四边形各边中点所得四边形是菱形.
解答:解:如图,∵E、F、G、H分别是线段AB、BC、CD、AD的中点,
∴EH、FG分别是△ABD、△BCD的中位线,EF、HG分别是△ACD、△ABC的中位线,
根据三角形的中位线的性质知,EH=FG=
BD,EF=HG=
AC,
又∵AC=BD,
∴EH=FG=EF=HG,
∴四边形EFGH是菱形.
∴EH、FG分别是△ABD、△BCD的中位线,EF、HG分别是△ACD、△ABC的中位线,
根据三角形的中位线的性质知,EH=FG=
| 1 |
| 2 |
| 1 |
| 2 |
又∵AC=BD,
∴EH=FG=EF=HG,
∴四边形EFGH是菱形.
点评:此题主要考查了三角形中位线定理和菱形的判定方法,题目比较典型,又有综合性,难度不大.

练习册系列答案
相关题目
 15、如图,已知四边形ABCD是等腰梯形,AB=DC,AD∥BC,PB=PC.求证:PA=PD.
15、如图,已知四边形ABCD是等腰梯形,AB=DC,AD∥BC,PB=PC.求证:PA=PD.
 的延长线分别交于点F、E,且
的延长线分别交于点F、E,且 (2013•梧州)如图,已知:AB∥CD,BE⊥AD,垂足为点E,CF⊥AD,垂足为点F,并且AE=DF.
(2013•梧州)如图,已知:AB∥CD,BE⊥AD,垂足为点E,CF⊥AD,垂足为点F,并且AE=DF.
