题目内容
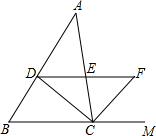 如图所示,△ABC中,∠ACB的平分线交AB于点D,过点D作BC的平行线交AC于点E,交∠ACB的外角平分线于点F.
如图所示,△ABC中,∠ACB的平分线交AB于点D,过点D作BC的平行线交AC于点E,交∠ACB的外角平分线于点F.
求证:(1)△DCF是直角三角形;(2)DE=EF.
证明:(1)∵DC平分∠ACB,CF平分∠ACM,
∴∠ACD= ∠ACB,∠ACF=
∠ACB,∠ACF= ∠ACM,
∠ACM,
∴∠DCF=∠ACD+∠ACF= (∠ACB+∠ACM)=90°,
(∠ACB+∠ACM)=90°,
∴△DCF是直角三角形;
(2)∵DF∥BC,
∴∠EDC=∠BCD,∠F=∠FCM,
∵DC平分∠ACB,CF平分∠ACM,
∴∠ACD=∠BCD,∠ACF=∠FCM,
∴∠EDC=∠ACD,∠F=∠ACF,
∴ED=EC,EC=EF,
∴DE=EF.
分析:(1)由DC平分∠ACB,CF平分∠ACM,根据角平分线的定义,可求得∠DCF=90°,即△DCF是直角三角形;
(2)由DF∥BC,DC平分∠ACB,CF平分∠ACM,易得△CDE与△CEF是等腰三角形,继而证得结论.
点评:此题考查了等腰三角形的判定与性质以及角平分线的定义.此题难度适中,注意掌握数形结合思想的应用.
∴∠ACD=
 ∠ACB,∠ACF=
∠ACB,∠ACF= ∠ACM,
∠ACM,∴∠DCF=∠ACD+∠ACF=
 (∠ACB+∠ACM)=90°,
(∠ACB+∠ACM)=90°,∴△DCF是直角三角形;
(2)∵DF∥BC,
∴∠EDC=∠BCD,∠F=∠FCM,
∵DC平分∠ACB,CF平分∠ACM,
∴∠ACD=∠BCD,∠ACF=∠FCM,
∴∠EDC=∠ACD,∠F=∠ACF,
∴ED=EC,EC=EF,
∴DE=EF.
分析:(1)由DC平分∠ACB,CF平分∠ACM,根据角平分线的定义,可求得∠DCF=90°,即△DCF是直角三角形;
(2)由DF∥BC,DC平分∠ACB,CF平分∠ACM,易得△CDE与△CEF是等腰三角形,继而证得结论.
点评:此题考查了等腰三角形的判定与性质以及角平分线的定义.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
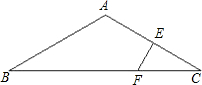 如图所示,△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线EF交AC于点E,交BC于点F.求证:BF=2CF.
如图所示,△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线EF交AC于点E,交BC于点F.求证:BF=2CF. 16、如图所示,△ABC中,∠C=90°,DE垂直平分斜边AB,分别交AB、AC于D、E,∠CAE:∠EAB=5:2,则∠B=
16、如图所示,△ABC中,∠C=90°,DE垂直平分斜边AB,分别交AB、AC于D、E,∠CAE:∠EAB=5:2,则∠B=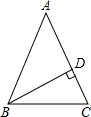 如图所示,△ABC中,AB=AC=10,BD是AC边的高线,DC=2,试求BD的长.
如图所示,△ABC中,AB=AC=10,BD是AC边的高线,DC=2,试求BD的长. 如图所示,△ABC中,BC的垂直平分线交AB于点E,若△ABC的周长为10,BC=4,则△ACE的周长是
如图所示,△ABC中,BC的垂直平分线交AB于点E,若△ABC的周长为10,BC=4,则△ACE的周长是 如图所示,△ABC中,AB=AC,BD⊥AC,垂足为D,求∠DBC与∠A的关系.
如图所示,△ABC中,AB=AC,BD⊥AC,垂足为D,求∠DBC与∠A的关系.