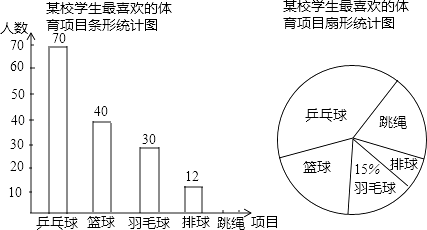
题目内容
【题目】如图,点A在反比例函数y=﹣ ![]() (x<0)的图象上移动,连接OA,作OB⊥OA,并满足∠OAB=30°.在点A的移动过程中,追踪点B形成的图象所对应的函数表达式为( )
(x<0)的图象上移动,连接OA,作OB⊥OA,并满足∠OAB=30°.在点A的移动过程中,追踪点B形成的图象所对应的函数表达式为( ) 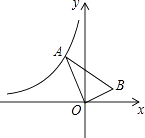
A.y= ![]() (x>0)
(x>0)
B.y= ![]() (x>0)
(x>0)
C.y= ![]() (x>0)
(x>0)
D.y= ![]() (x>0)
(x>0)
【答案】B
【解析】解:设B点坐标满足的函数解析式是y= ![]() , 过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D,
, 过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D,
∴∠ACO=∠BDO=90°,
∴∠AOC+∠OAC=90°,
∵∠AOB=90°,
∴∠AOC+∠BOD=90°,
∴∠BOD=∠OAC,
∴△AOC∽△OBD,
∴S△AOC:S△BOD=( ![]() )2 ,
)2 ,
∵AO= ![]() BO,
BO,
∴S△AOC:S△BOD=3,
∵S△AOC= ![]() OCAC=
OCAC= ![]() ,S△BOD=
,S△BOD= ![]() ,
,
∴设B点坐标满足的函数解析式是y= ![]() .
.
故选B.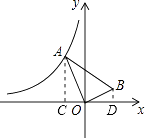

练习册系列答案
相关题目