МвДїДЪИЭ
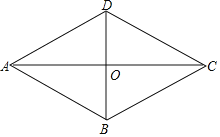
ЎѕМвДїЎїИзНјЈ¬КэЦбЙПAµг±нКѕКэaЈ¬ЛьУлФµгµДѕаАлКЗ2ёцµҐО»і¤¶ИЈ¬Bµг±нКѕКэbЈ¬ЛьУлФµгµДѕаАлКЗ4ёцµҐО»і¤¶И.
(1)![]() Ј»
Ј»![]() Ј»
Ј»
(2)ТСЦЄјЧґУAґ¦іц·ўЈ¬Н¬К±ТТґУBґ¦іц·ўЈ¬ЙиФЛ¶ЇµДК±јдОЄ![]() ЈЁГлЈ©Ј¬
ЈЁГлЈ©Ј¬
ўЩИфјЧПтУТЈ¬ТТПтЧуФЛ¶ЇЈ¬ЛЩ¶ИѕщОЄ2ёцµҐО»/ГлЈ¬µ±![]() К±Ј¬јЧУлФµгµДѕаАлКЗ Ј»ТТУлФµгµДѕаАлКЗ Ј»
К±Ј¬јЧУлФµгµДѕаАлКЗ Ј»ТТУлФµгµДѕаАлКЗ Ј»
ўЪИфјЧЎўТТѕщПтЧуФЛ¶ЇЈ¬јЧµДЛЩ¶ИОЄmёцµҐО»/ГлЈ¬ТТµДЛЩ¶ИОЄnёцµҐО»/ЎЎЎЎ ГлЈ¬µ±![]() К±Ј¬УГґъКэКЅ±нКѕјЧЎўТТЛщ±нКѕµДКэ.
К±Ј¬УГґъКэКЅ±нКѕјЧЎўТТЛщ±нКѕµДКэ.
![]()
Ўѕґр°ёЎї(1)![]() Ј» (2)ўЩ
Ј» (2)ўЩ![]() Ј» ўЪјЧЛщ±нКѕµДКэОЄЈє
Ј» ўЪјЧЛщ±нКѕµДКэОЄЈє![]() Ј» ТТЛщ±нКѕµДКэОЄЈє
Ј» ТТЛщ±нКѕµДКэОЄЈє![]() .
.
ЎѕЅвОцЎї
ЈЁ1Ј©ёщѕЭКэЦбЙПµДµг±нКѕµДКэУлЖдµЅФµгµДѕаАлµД№ШПµЅвґрјґїЙ
ЈЁ2Ј©јЧ±ѕЙнУлФµгПаёф2ёцµҐО»і¤¶ИЈ¬ФЪёє°лЦбЈ¬НщУТФЛ¶Ї4ГлєуЈ¬УГФЛ¶ЇµДѕаАлјхИҐ±ѕЙнУлФµгµДѕаАл±гїЙЗуіцґЛК±ѕаФµгµДѕаАлЈ»ТТ±ѕЙнУлФµгПаёф4ёцµҐО»і¤¶ИЈ¬ФЪХэ°лЦбЈ¬НщЧуФЛ¶ЇЛДГлєуЈ¬УГФЛ¶ЇµДѕаАлјхИҐ±ѕЙнУлФµгµДѕаАл±гїЙЗуіцґЛК±ѕаФµгµДѕаАл
ЈЁ3Ј©јЧ±ѕЙн±нКѕµДОЄ©Ѓ2Ј¬НщЧуФЛ¶ЇЈ¬ФтКЗФЪ±ѕЙнµДЦµЙПјхИҐФЛ¶ЇµДѕаАл±гїЙµГФЛ¶ЇєуЛщ±нКѕµДКэЈ»ТТµДЛг·ЁёъјЧТ»Сщ
ЅвЈє(1)![]() Ј»
Ј»
(2)ўЩ![]() Ј»
Ј»
ўЪјЧЛщ±нКѕµДКэОЄЈє![]() Ј»
Ј»
ТТЛщ±нКѕµДКэОЄЈє![]() .
.

 ГїїО±ШБ·ПµБРґр°ё
ГїїО±ШБ·ПµБРґр°ё ЗЙС§ЗЙБ·ПµБРґр°ё
ЗЙС§ЗЙБ·ПµБРґр°ёЎѕМвДїЎїУРХвСщТ»ёцОКМвЈєМЅѕїєЇКэy=![]() µДНјПуУлРФЦКЎЈРЎ»ЫёщѕЭС§П°єЇКэµДѕСйЈ¬¶ФєЇКэy=
µДНјПуУлРФЦКЎЈРЎ»ЫёщѕЭС§П°єЇКэµДѕСйЈ¬¶ФєЇКэy=![]() µДНјПуУлРФЦКЅшРРБЛМЅѕїЎЈПВГжКЗРЎ»ЫµДМЅѕї№эіМЈ¬ЗлІ№ідНкіЙЈє
µДНјПуУлРФЦКЅшРРБЛМЅѕїЎЈПВГжКЗРЎ»ЫµДМЅѕї№эіМЈ¬ЗлІ№ідНкіЙЈє
ЈЁ1Ј©єЇКэy=![]() µДЧФ±дБїxµДИЎЦµ·¶О§КЗ__________Ј»
µДЧФ±дБїxµДИЎЦµ·¶О§КЗ__________Ј»
ЈЁ2Ј©БРіцyУлxµДјёЧй¶ФУ¦ЦµЎЈЗлЦ±ЅУРґіцmµДЦµЈ¬m=________Ј»
x | Ў | -3 | -2 | 0 | 1 | 1.5 | 2.5 | m | 4 | 6 | 7 | Ў |
y | Ў | 2.4 | 2.5 | 3 | 4 | 6 | -2 | 0 | 1 | 1.5 | 1.6 | Ў |
ЈЁ3Ј©ЗлФЪЖЅГжЦ±ЅЗЧш±кПµxOyЦРЈ¬ГиіцТФЙП±нЦРёч¶Ф¶ФУ¦ЦµОЄЧш±кµДµгЈ¬Іў»іцёГєЇКэµДНјПуЈ»
ЈЁ4Ј©ЅбєПєЇКэµДНјПуЈ¬РґіцёГєЇКэµДБЅМхРФЦКЈє
ўЩ_____________________________________________Ј»
ўЪ____________________________________________ЎЈ