题目内容
如图,在平面直角坐标系中,直线y=-
x+8分别与x轴交于点A,与y轴交于点B,∠OAB的平分线交y轴于点E,点C在线段AB上,以CA为直径的⊙D经过点E.
(1)判断⊙D与y轴的位置关系,并说明理由;
(2)求点C的坐标.

| 4 |
| 3 |
(1)判断⊙D与y轴的位置关系,并说明理由;
(2)求点C的坐标.

(1)相切,连接ED,
∵∠OAB的平分线交y轴于点E,
∴∠DAE=∠EAO.
∵∠DEA=∠DAE,
∴∠DEA=∠DAE=∠EAO,
所以ED∥OA,
所以ED⊥OB;
(2)做CM⊥BO,CF⊥AO,
易得AB=10.设C(m,n),ED=R,
则DE⊥BO,
∴ED∥AO,
△BED∽△BOA,
=
,
=
,
解得:R=
,
∴△AFC∽△AOB,
∴
=
,
∴
=
,
解得:CF=6,
利用勾股定理可求出AF=4.5,
∴OF=1.5,
所以C(
,6).
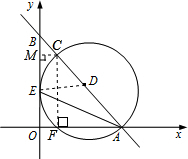
∵∠OAB的平分线交y轴于点E,
∴∠DAE=∠EAO.
∵∠DEA=∠DAE,
∴∠DEA=∠DAE=∠EAO,
所以ED∥OA,
所以ED⊥OB;
(2)做CM⊥BO,CF⊥AO,
易得AB=10.设C(m,n),ED=R,
则DE⊥BO,
∴ED∥AO,
△BED∽△BOA,
| DE |
| AO |
| BD |
| AB |
| R |
| 6 |
| 10-R |
| 10 |
解得:R=
| 15 |
| 4 |
∴△AFC∽△AOB,
∴
| CF |
| BO |
| AC |
| AB |
∴
| CF |
| 8 |
| 7.5 |
| 10 |
解得:CF=6,
利用勾股定理可求出AF=4.5,
∴OF=1.5,
所以C(
| 3 |
| 2 |
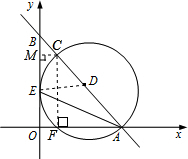

练习册系列答案
相关题目
 A在y轴的正半轴上,E是边AB上的一点,直线EC交y轴于F,且S△FAE:S四边形AOCE=1:3.
A在y轴的正半轴上,E是边AB上的一点,直线EC交y轴于F,且S△FAE:S四边形AOCE=1:3.
 >a)收费.设一户居民月用水x吨,应收水费y元,y与x之间的函数关系如图所示.
>a)收费.设一户居民月用水x吨,应收水费y元,y与x之间的函数关系如图所示.

