��Ŀ����
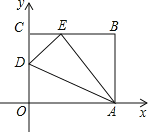
����Ŀ��������ͬһ��ͼ�ε�����ò�ͬ��ʽ��ʾ������֤��һ�ຬ���߶εĵ�ʽ�����ֽ������ķ������dz�֮Ϊ���������ѧ�����ã��ڵ���������ABC�У�AB=AC����һ���ϵĸ�BD=h��M�ǵױ�BC�ϵ�����һ�㣬M����AB�ľ���ME=h1��M����AC�ľ���MF=h2��
��1��������ͼ��1��֤����h1+h2=h��
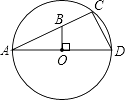
��2������M��BC���ӳ�����ʱ��h1��h2��h֮������ʲô���Ľ��ۣ�������ͼ2�л���ͼ�Σ�
��3�����������Ͻ��۽���������⣬��ͼ3����ƽ��ֱ������ϵ��������ֱ��l1��y=![]() ��l2��y=��3x+3����l2�ϵ�һ��M��l1�ľ�����1�����M�����꣮
��l2��y=��3x+3����l2�ϵ�һ��M��l1�ľ�����1�����M�����꣮

���𰸡���1��h1+h2=h����2��h1��h2=h��ͼ�����������3����M������ΪM��![]() ��2����
��2����![]() ��4����
��4����
��������
��1������S��ABC=S��ABM+S��AMC��������𰸣�
��2��h1-h2=h��
��3���������ABCΪ���������Σ��ٸ��ݣ�1����2���Ľ���֢ٵ���M��BC����ʱ���ڵ���M��CB�ӳ�����ʱ�����M�����꣮�۵���M��BC���ӳ�����ʱ��h1=1��h�������ڣ�
��1������AM���������h1=ME��h2=MF��h=BD��
��S��ABC=S��ABM+S��AMC��
S��ABM=![]() ��AB��ME=
��AB��ME=![]() ��AB��h1��
��AB��h1��
S��AMC=![]() ��AC��MF=
��AC��MF=![]() ��AC��h2��
��AC��h2��
�֡�S��ABC=![]() ��AC��BD=
��AC��BD=![]() ��AC��h��AB=AC��
��AC��h��AB=AC��
��![]() ��AC��h=
��AC��h=![]() ��AB��h1+
��AB��h1+![]() ��AC��h2��
��AC��h2��
��h1+h2=h��
��2����ͼ��ʾ��

h1��h2=h��
��3����y=![]() x+3����x=0��y=3����y=0��x=��4��
x+3����x=0��y=3����y=0��x=��4��
����A����4��0����B��0��3��ͬ�����C��1��0����
AB=![]() =5��AC=5������AB=AC��
=5��AC=5������AB=AC��
����ABC����������
�ٵ���M��BC����ʱ����h1+h2=h�ã�1+My=OB��My=3��1=2��
��������y=��3x+3����ã�Mx=![]() ��
��
���Դ�ʱM��![]() ��2����
��2����
�ڵ���M��CB�ӳ�����ʱ����h1��h2=h�ã�My��1=OB��My=3+1=4��
��������y=��3x+3����ã�Mx=��![]() ��
��
���Դ�ʱM����![]() ��4����
��4����
�۵���M��BC���ӳ�����ʱ��h1=1��h�������ڣ�
������������M������ΪM��![]() ��2����
��2����![]() ��4����
��4����