题目内容
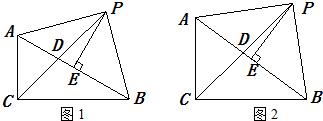
24、(1)已知:如图1,Rt△ABC中,∠ACB=90°,∠BAC=60°,CD平分∠ACB,点E为AB中点,PE⊥AB交CD的延长线于P,猜想:∠PAC+∠PBC=
(2)已知:如图2,Rt△ABC中,∠ACB=90°,∠BAC≠45°,CD平分∠ACB,点E为AB中点,PE⊥AB交CD的延长线于P,(1)中结论是否成立,若成立,请证明;若不成立请说明理由.
180°
°(直接写出结论,不需证明).(2)已知:如图2,Rt△ABC中,∠ACB=90°,∠BAC≠45°,CD平分∠ACB,点E为AB中点,PE⊥AB交CD的延长线于P,(1)中结论是否成立,若成立,请证明;若不成立请说明理由.

分析:(1)根据三角形和四边形的内角和定理可猜想:∠PAC+∠PBC=180°;
(2)连接CE,如能够证明CE=PE=EB=AE,即可得△PAE与△PBE为等腰直角三角形,则∠APB=45°+45°=90°,再由四边形的内角和即可得证;由已知易证AE=EB=EC,主要是证明PE=EC=AE,可由∠EAC=∠ECA,则∠DCE=∠ECA-∠DCA=∠EAC-45°,又∵∠DAC=180°-∠ADC-45°=135°-∠PDE,
∴∠DCE=135°-∠PDE-45°=90°-∠PDE=∠DPE,即可得证.
(2)连接CE,如能够证明CE=PE=EB=AE,即可得△PAE与△PBE为等腰直角三角形,则∠APB=45°+45°=90°,再由四边形的内角和即可得证;由已知易证AE=EB=EC,主要是证明PE=EC=AE,可由∠EAC=∠ECA,则∠DCE=∠ECA-∠DCA=∠EAC-45°,又∵∠DAC=180°-∠ADC-45°=135°-∠PDE,
∴∠DCE=135°-∠PDE-45°=90°-∠PDE=∠DPE,即可得证.
解答:解:(1)猜想:∠PAC+∠PBC=180° ;
;
(2)结论:依然成立.
证明:连接CE.
∵E为AB中点,
∴AE=EB=EC,
∴∠EAC=∠ECA,
∴∠DCE=∠ECA-∠DCA=∠EAC-45°,
又∵∠DAC=180°-∠ADC-45°=135°-∠PDE,
∴∠DCE=135°-∠PDE-45°=90°-∠PDE=∠DPE,
∴PE=EC=AE,
∴△PAE与△PBE为等腰直角三角形,∠APB=90°,
∴∠PAC+∠PBC=360°-∠APB-∠ACB=360°-90°-90°=180°.
 ;
;(2)结论:依然成立.
证明:连接CE.
∵E为AB中点,
∴AE=EB=EC,
∴∠EAC=∠ECA,
∴∠DCE=∠ECA-∠DCA=∠EAC-45°,
又∵∠DAC=180°-∠ADC-45°=135°-∠PDE,
∴∠DCE=135°-∠PDE-45°=90°-∠PDE=∠DPE,
∴PE=EC=AE,
∴△PAE与△PBE为等腰直角三角形,∠APB=90°,
∴∠PAC+∠PBC=360°-∠APB-∠ACB=360°-90°-90°=180°.
点评:此题综合考查角平分线的定义、等腰直角三角形的判定、直角三角形的性质和三角形、四边形的内角和等知识点,难度较大,辅助线的作法是关键.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
 ,测得C在B的北偏西45°方向上.
,测得C在B的北偏西45°方向上. 11、已知,如图,正比例函数与反比例函数的图象相交于A、B两点,A点坐标为(2,1),分别以A、B为圆心的圆与x轴相切,则图中两个阴影部分面积的和为
11、已知,如图,正比例函数与反比例函数的图象相交于A、B两点,A点坐标为(2,1),分别以A、B为圆心的圆与x轴相切,则图中两个阴影部分面积的和为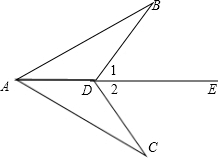 已知,如图,∠1=∠2,
已知,如图,∠1=∠2, 已知,如图,直角坐标系内的矩形ABCD,顶点A的坐标为(0,3),BC=2AB,P为
已知,如图,直角坐标系内的矩形ABCD,顶点A的坐标为(0,3),BC=2AB,P为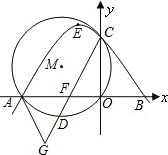 于C点,⊙M经过原点O及点A、C,点D是劣弧
于C点,⊙M经过原点O及点A、C,点D是劣弧