题目内容
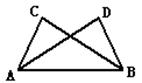
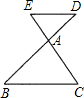 如图,已知
如图,已知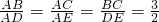 ,则:(1)
,则:(1)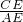 =______,(2)若BD=10cm,则AD=______cm;(3)若△ADE的周长为16cm,则△ABC的周长为______cm.
=______,(2)若BD=10cm,则AD=______cm;(3)若△ADE的周长为16cm,则△ABC的周长为______cm.
解:(1)根据题意,设根据比例式设AC=3k,AE=2k,有CE=5k,
∴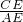 =5k:2k=
=5k:2k= ;
;
(2)根据题意,设AB=3k,AD=2k,
∴BD=AB+AD=5k=10,
∴k=2,
∴AD=2k=4cm;
(3)∵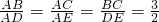 ,
,
∴△ABC∽△ADE,
∴△ABC的周长:△ADE的周长=3:2,
∵△ADE的周长为16cm,
∴△ABC的周长为24cm.
故本题答案为: ;4cm;24cm.
;4cm;24cm.
分析:(1)根据比例式设AC=3k,AE=2k,有CE=5k,代入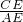 计算;
计算;
(2)根据比例式设AB=3k,AD=2k,则5k=10,解得k=2,则可求得AD的值;
(3)根据三组对应边的比相等得到两个三角形相似,再根据相似三角形周长的比等于相似比,所以其周长是16× =24cm.
=24cm.
点评:综合运用了相似三角形的判定和性质.
∴
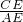 =5k:2k=
=5k:2k= ;
;(2)根据题意,设AB=3k,AD=2k,
∴BD=AB+AD=5k=10,
∴k=2,
∴AD=2k=4cm;
(3)∵
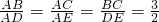 ,
,∴△ABC∽△ADE,
∴△ABC的周长:△ADE的周长=3:2,
∵△ADE的周长为16cm,
∴△ABC的周长为24cm.
故本题答案为:
 ;4cm;24cm.
;4cm;24cm.分析:(1)根据比例式设AC=3k,AE=2k,有CE=5k,代入
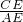 计算;
计算;(2)根据比例式设AB=3k,AD=2k,则5k=10,解得k=2,则可求得AD的值;
(3)根据三组对应边的比相等得到两个三角形相似,再根据相似三角形周长的比等于相似比,所以其周长是16×
 =24cm.
=24cm.点评:综合运用了相似三角形的判定和性质.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
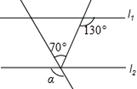
如图,已知直线 则∠
则∠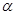
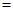 ( )
( )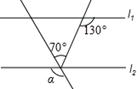
| A. 150° | B. 140° | C. 130° | D. 120° |
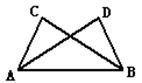
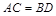 ,则再添加条件_______,可证出
,则再添加条件_______,可证出 ≌
≌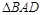 .
.
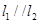 则∠
则∠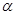
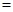 ( )
( )
 ,则(1)
,则(1)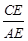 =______,(2)若BD=10cm,则AD=______;(3)若△ADE的周长为16cm,则△ABC的周长为_______.
=______,(2)若BD=10cm,则AD=______;(3)若△ADE的周长为16cm,则△ABC的周长为_______.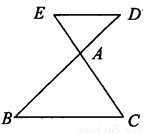
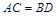 ,则再添加条件_______,可证出
,则再添加条件_______,可证出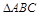 ≌
≌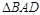 .
.