题目内容
已知:如图①,tan∠MON= ,点A是OM上一定点,AC⊥ON于点C,AC=4cm,点B在线段OC上,且tan∠ABC=2.点P从点O出发,以每秒
,点A是OM上一定点,AC⊥ON于点C,AC=4cm,点B在线段OC上,且tan∠ABC=2.点P从点O出发,以每秒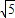 cm的速度在射线OM上匀速运动,点Q、R在射线ON上,且PQ∥AB,PR∥AC.设点P运动了x秒.
cm的速度在射线OM上匀速运动,点Q、R在射线ON上,且PQ∥AB,PR∥AC.设点P运动了x秒.(1)用x表示线段OP的长为______
【答案】分析:(1)利用勾股定理即可求出OR的长
(2)当R与B重合时△PQR与△ABC开始重叠,当Q与C重合时△PQR与△ABC不再重叠,根据上述极限位置列方程求解.
(3)根据(2)中函数关系,令其等于 解出对应的x值即可.
解出对应的x值即可.
解答:解:(1)OP的长为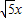 ,OR的长为2x.
,OR的长为2x.
(2)函数关系式为.①当3<x<4时,S=(2x-6)2
②当4≤x<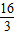 ,S=
,S=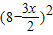 =
= x2-24x+64;
x2-24x+64;
(3)当S= 时
时
①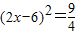 ,解得x=
,解得x=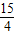
②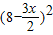 =
= ,解得x=
,解得x=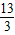
故当点P运动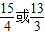 秒时,△PQR与△ABC重叠部分的面积为
秒时,△PQR与△ABC重叠部分的面积为 .
.
点评:考查三角形面积计算以及分类讨论的能力,综合性较强,关键思路需清晰.
(2)当R与B重合时△PQR与△ABC开始重叠,当Q与C重合时△PQR与△ABC不再重叠,根据上述极限位置列方程求解.
(3)根据(2)中函数关系,令其等于
 解出对应的x值即可.
解出对应的x值即可.解答:解:(1)OP的长为
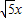 ,OR的长为2x.
,OR的长为2x.(2)函数关系式为.①当3<x<4时,S=(2x-6)2
②当4≤x<
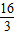 ,S=
,S=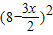 =
= x2-24x+64;
x2-24x+64;(3)当S=
 时
时①
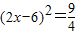 ,解得x=
,解得x=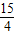
②
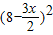 =
= ,解得x=
,解得x=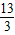
故当点P运动
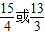 秒时,△PQR与△ABC重叠部分的面积为
秒时,△PQR与△ABC重叠部分的面积为 .
.点评:考查三角形面积计算以及分类讨论的能力,综合性较强,关键思路需清晰.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
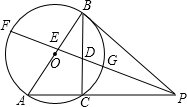 已知:如图,AB是⊙O的直径,PB切⊙O于点B,PA交⊙O于点C,∠A=60°,∠APB的平分线PF分别交BC、AB于点D、E,交⊙O于点F、G,且BD•AE=2
已知:如图,AB是⊙O的直径,PB切⊙O于点B,PA交⊙O于点C,∠A=60°,∠APB的平分线PF分别交BC、AB于点D、E,交⊙O于点F、G,且BD•AE=2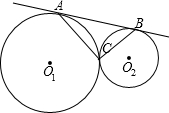 已知:如图,⊙O1与⊙O2外切于C点,AB一条外公切线,A、B分别为切点,连接AC、BC.设⊙O1的半径为R,⊙O2的半径为r,若tan∠ABC=
已知:如图,⊙O1与⊙O2外切于C点,AB一条外公切线,A、B分别为切点,连接AC、BC.设⊙O1的半径为R,⊙O2的半径为r,若tan∠ABC=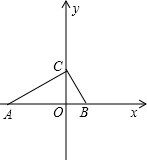 15,∠CBA>∠CAB,且tan∠CAB、tan∠CBA是关于x的方程x2+mx+n=0的两根,
15,∠CBA>∠CAB,且tan∠CAB、tan∠CBA是关于x的方程x2+mx+n=0的两根, d,试判断d+AB的值是否会发生变化,若不变,求出其值;若变化,求其变化的范围.
d,试判断d+AB的值是否会发生变化,若不变,求出其值;若变化,求其变化的范围. 已知:如图,点B在y轴的负半轴上,点A在x轴的正半轴上,且OA=2,tan∠OAB=2.
已知:如图,点B在y轴的负半轴上,点A在x轴的正半轴上,且OA=2,tan∠OAB=2.