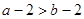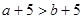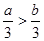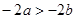题目内容
设a、b、c为 的三边,试说明
的三边,试说明 .(本题6分)
.(本题6分)
 的三边,试说明
的三边,试说明 .(本题6分)
.(本题6分)解:将不等式的左边因式分解得(a+b+c)(a-b-c),
根据题意,可知: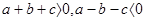

根据题意,可知:

略
解:这个题第一步由a2-b2-c2-2bc=(a+b+c)(a-b-c)时,用到了知识点平方差公式a2-b2=(a+b)(a-b),完全平方公式a2+2ab+b2=(a+b)2,即先把原式化为a2-(b2+c2+2bc)=a2-(b+c)2=(a+b+c)(a-b-c)。第二步由三角形三边的关系可以得到a+b+c>0,a-b-c<0,所以(a+b+c)(a-b-c)<0,即原式=(a+b+c)(a-b-c)<0,所以a2-b2-c2-2bc<0
解:这个题第一步由a2-b2-c2-2bc=(a+b+c)(a-b-c)时,用到了知识点平方差公式a2-b2=(a+b)(a-b),完全平方公式a2+2ab+b2=(a+b)2,即先把原式化为a2-(b2+c2+2bc)=a2-(b+c)2=(a+b+c)(a-b-c)。第二步由三角形三边的关系可以得到a+b+c>0,a-b-c<0,所以(a+b+c)(a-b-c)<0,即原式=(a+b+c)(a-b-c)<0,所以a2-b2-c2-2bc<0

练习册系列答案
相关题目
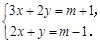 当m为何值时,x>y?
当m为何值时,x>y? 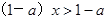 的解集是x<1,则a的范围是
的解集是x<1,则a的范围是 
 吨, 则粗加工的吨数为 吨,加工这批海产品需要 天, 可获利 元(用含
吨, 则粗加工的吨数为 吨,加工这批海产品需要 天, 可获利 元(用含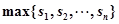 表示实数
表示实数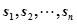 中的最大者.设
中的最大者.设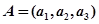 ,
,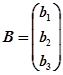 ,记
,记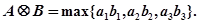 设
设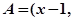
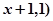 ,
,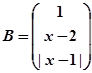 ,若
,若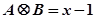 ,则
,则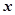 的取值范围为( )
的取值范围为( )







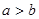 ,则下列结论一定错误的是
,则下列结论一定错误的是