题目内容
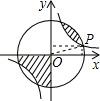
如图所示,点P(3a,a)是反比例函数y= (k>0)与⊙O的一个交点,图中阴影部分的面积为10π,则反比例函数的解析式为( )
(k>0)与⊙O的一个交点,图中阴影部分的面积为10π,则反比例函数的解析式为( )

 (k>0)与⊙O的一个交点,图中阴影部分的面积为10π,则反比例函数的解析式为( )
(k>0)与⊙O的一个交点,图中阴影部分的面积为10π,则反比例函数的解析式为( )
A.y= | B.y= | C.y= | D.y= |
D
试题分析:根据P(3a,a)和勾股定理,求出圆的半径,进而表示出圆的面积,再根据圆的面积等于阴影部分面积的四倍,求出圆的面积,建立等式即可求出a的值,从而得出反比例函数的解析式.
解:由于函数图象关于原点对称,所以阴影部分面积为
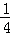 圆面积,
圆面积,则圆的面积为10π×4=40π.
因为P(3a,a)在第一象限,则a>0,3a>0,
根据勾股定理,OP=
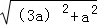 =
=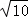 a.
a.于是π
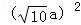 =40π,a=±2,(负值舍去),故a=2.
=40π,a=±2,(负值舍去),故a=2.P点坐标为(6,2).
将P(6,2)代入y=
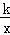 ,
,得:k=6×2=12.
反比例函数解析式为:y=
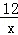 .
.故选D.
点评:此题是一道综合题,既要能熟练正确求出圆的面积,又要会用待定系数法求函数的解析式.

练习册系列答案
相关题目
 ;
; .
.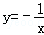 的图象上,则用“>”连接y1、y2、y3得 .
的图象上,则用“>”连接y1、y2、y3得 . (x>0)的图象上时,设△ABC在第一象限部分的面积分别记做S1、S2(如图1、图2所示)D是斜边与y轴的交点,通过计算比较S1、S2的大小.
(x>0)的图象上时,设△ABC在第一象限部分的面积分别记做S1、S2(如图1、图2所示)D是斜边与y轴的交点,通过计算比较S1、S2的大小.
 的图象在同一平面直角坐标系中是( )
的图象在同一平面直角坐标系中是( )



 的对称性叙述错误的是( )
的对称性叙述错误的是( )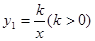 与直线
与直线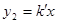 交于A,B两点,点A在第一象限.试解答下列问题:
交于A,B两点,点A在第一象限.试解答下列问题: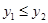 ;
;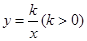 于P,Q两点,点P在第一象限, 如图2所示.
于P,Q两点,点P在第一象限, 如图2所示.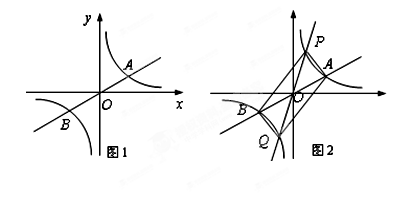
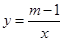 的图象如图,则m的取值范围是 .
的图象如图,则m的取值范围是 .