Question

如图，已知半圆O的直径AB，将一个三角板的直角顶点固定在圆心O上，当三角板绕着点O转动时，三角板的两条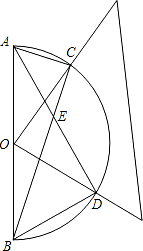直角边与半圆圆周分别交于C、D两点，连接AD、BC交于点E．
（1）求证：△ACE∽△BDE；
（2）求证：BD=DE恒成立．

Answer 1

分析：（1）根据圆周角定理及对顶角相等可知∠CAE=∠DBE，∠AEC=∠BED，故可得出结论；
（2）由直角三角板的性质可知∠COD=90°，由圆周角定理可知∠DBE=∠DEB=45°，故△BDE是等腰直角三角形，故BD=DE恒成立．

解答：证明：（1）∵∠CAE=∠DBE，∠AEC=∠BED
∴△ACE∽△BDE；

（2）∵∠COD=90°
∴∠DBE=

1

2

×90°=45°，
∵AB为直径，
∴∠BDE=90°，
∴∠DEB=∠DBE=45°，
∴BD=DE恒成立．

点评：本题考查的是相似三角形的判定，圆周角定理及等腰三角形的性质，根据题意判断出△BDE是等腰直角三角形是解答此题的关键．