题目内容
如图①,点A′,B′的坐标分别为(2,0)和(0,-4),将△A′B′O绕点O按逆时针方向旋转90°后得△ABO,点A′的对应点是点A,点B′的对应点是点B.
(1)写出A,B两点的坐标,并求出直线AB的解析式;
(2)将△ABO沿着垂直于x轴的线段CD折叠,(点C在x轴上,点D在AB上,点D不与A,B重合)如图②,使点B落在x轴上,点B的对应点为点E.设点C的坐标为(x,0),△CDE与△ABO重叠部分的面积为S.
①试求出S与x之间的函数关系式(包括自变量x的取值范围);
②当x为何值时,S的面积最大,最大值是多少?
③是否存在这样的点C,使得△ADE为直角三角形?若存在,直接写出点C的坐标; 若不存在,请说明理由.
若不存在,请说明理由.
解:
(1)A(0,2),B(4,0)
设直线AB的解析式y=kx+b,则有
解得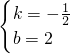
∴直线AB的解析式为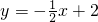
(2)i)①点E在原点和x轴正半轴上时,重叠部分是△CDE.
则S△CDE=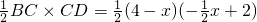
=
当E与O重合时,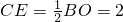
∴2≤x<4
②当E在x轴的负半轴上时,设DE与y轴交于点F,则重叠部分为梯形
∵△OFE∽△OAB
∴ ,
,
∴
又∵OE=4-2x
∴
∴

=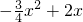
当点C与点O重合时,点C的坐标为(0,0)
∴0<x<2
综合①②得
ii)①当2≤x<4时,
∴对称轴是直线x=4
∵抛物线开口向上,
∴在2≤x<4中,S随x的增大而减小
∴当x=2时,S的最大值=
②当0<x<2时,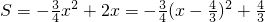
∴对称轴是直线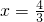
∵抛物线开口向下∴当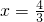 时,S有最大值为
时,S有最大值为
综合①②当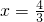 时,S有最大值为
时,S有最大值为
iii)存在,点C的坐标为( ,0)和(
,0)和( ,0)
,0)
附:详解:①当△ADE以点A为直角顶点时,作AE⊥AB交x轴负半轴于点E,
∵△AOE∽△BOA
∴
∵AO=2∴EO=1
∴点E坐标为(-1,0)
∴点C的坐标为( ,0)②当△ADE以点E为直角顶点时
,0)②当△ADE以点E为直角顶点时
同样有△AOE∽△BOA
∴EO=1∴E(1,0)
∴点C的坐标( ,0)
,0)
综合①②知满足条件的坐标有( ,0)和(
,0)和( ,0).
,0).
以上仅提供本试题的一种解法或解题思路,若有不同解法请参照评分标准予以评分.
分析:(1)根据旋转的性质可以得到OA=OA′,OB=OB′,则A,B的坐标就可以得到,根据待定系数法就可以求出直线AB的解析式.
(2)①OB=4,C点的位置应分两种情况进行讨论,当C在OB的中点或在中点与B之间时,重合部分是△CDE;当C在OB的中点与O之间时,重合部分是梯形,就可以得到函数解析式.
②求出S与x之间的函数解析式,根据函数的性质就可以得到面积的最值.
③分△ADE以点A为直角顶点和△ADE以点E为直角顶点,两种情况进行讨论.根据相似三角形的对应边的比相等,求出OE的长,就可以得到C点的坐标.
点评:本题主要考查了待定系数法求函数的解析式,求函数的最值,以及相似三角形的对应边的比相等.
(1)A(0,2),B(4,0)
设直线AB的解析式y=kx+b,则有

解得
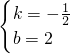
∴直线AB的解析式为
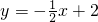
(2)i)①点E在原点和x轴正半轴上时,重叠部分是△CDE.
则S△CDE=
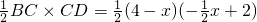
=

当E与O重合时,
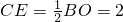
∴2≤x<4
②当E在x轴的负半轴上时,设DE与y轴交于点F,则重叠部分为梯形
∵△OFE∽△OAB
∴
 ,
,∴

又∵OE=4-2x
∴

∴


=
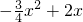
当点C与点O重合时,点C的坐标为(0,0)
∴0<x<2
综合①②得

ii)①当2≤x<4时,

∴对称轴是直线x=4
∵抛物线开口向上,
∴在2≤x<4中,S随x的增大而减小
∴当x=2时,S的最大值=

②当0<x<2时,
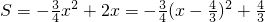
∴对称轴是直线
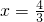
∵抛物线开口向下∴当
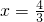 时,S有最大值为
时,S有最大值为
综合①②当
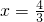 时,S有最大值为
时,S有最大值为
iii)存在,点C的坐标为(
 ,0)和(
,0)和( ,0)
,0)附:详解:①当△ADE以点A为直角顶点时,作AE⊥AB交x轴负半轴于点E,
∵△AOE∽△BOA
∴

∵AO=2∴EO=1
∴点E坐标为(-1,0)
∴点C的坐标为(
 ,0)②当△ADE以点E为直角顶点时
,0)②当△ADE以点E为直角顶点时同样有△AOE∽△BOA

∴EO=1∴E(1,0)
∴点C的坐标(
 ,0)
,0)综合①②知满足条件的坐标有(
 ,0)和(
,0)和( ,0).
,0).以上仅提供本试题的一种解法或解题思路,若有不同解法请参照评分标准予以评分.
分析:(1)根据旋转的性质可以得到OA=OA′,OB=OB′,则A,B的坐标就可以得到,根据待定系数法就可以求出直线AB的解析式.
(2)①OB=4,C点的位置应分两种情况进行讨论,当C在OB的中点或在中点与B之间时,重合部分是△CDE;当C在OB的中点与O之间时,重合部分是梯形,就可以得到函数解析式.
②求出S与x之间的函数解析式,根据函数的性质就可以得到面积的最值.
③分△ADE以点A为直角顶点和△ADE以点E为直角顶点,两种情况进行讨论.根据相似三角形的对应边的比相等,求出OE的长,就可以得到C点的坐标.
点评:本题主要考查了待定系数法求函数的解析式,求函数的最值,以及相似三角形的对应边的比相等.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目

 (2013•松江区模拟)已知:点A、B都在半径为9的圆O上,P是射线OA上一点,以PB为半径的圆P与圆O相交的另一个交点为C,直线OB与圆P相交的另一个交点为D,
(2013•松江区模拟)已知:点A、B都在半径为9的圆O上,P是射线OA上一点,以PB为半径的圆P与圆O相交的另一个交点为C,直线OB与圆P相交的另一个交点为D,

