题目内容
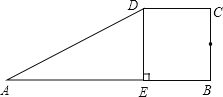
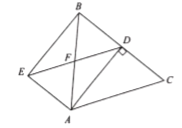
【题目】如图,在四边形ABCD中,AD//BC,∠A=∠C,CD=2AD,BE⊥AD于点E,F为CD的中点,连接EF、BF.
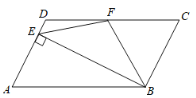
(1)求证:四边形ABCD是平行四边形;
(2)求证:BF平分∠ABC;
(3)请判断△BEF的形状,并证明你的结论.
【答案】(1)见解析;(2)见解析;(3)ΔBEF为等腰三角形,见解析.
【解析】
(1)由平行线的性质得出∠A+∠ABC=180°,由已知得出∠C+∠ABC=180°,证出AB//BC,即可得出四边形ABCD是平行四边形;
(2)由平行四边形的性质得出BC=AD,AB//CD,得出∠CFB=∠ABF,由已知得出CF=BC,得出∠CFB=∠CBF,证出∠ABF=∠CBF即可;
(3)作FG⊥BE于G,证出FG/AD//BC,得出EG=BG,由线段垂直平分线的性质得出EF=BF即可.
解:(1)证明:∵AD∥BC,
∴∠A+∠ABC=180°:
∵∠A=∠C
∴∠C+∠ABC=180°
∴AB∥CD
∴四边形ABCD是平行四边形
(2)证明:
∵F点为CD中点
∴CD=2CF
∴CD=2AD
∴CF=AD=BC
∴∠CFB=∠CBF
∴CD∥AB
∴∠CFB=∠FBA
∴∠FBA=∠CBF
∴BF平分∠ABC
(3)ΔBEF为等腰三角形
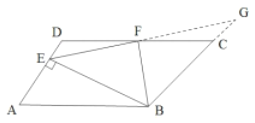
理由:如图,延长EF交B延长线于点G
∴DA∥BG
∴∠G=∠DEF
∵F为DC中点
∴DF=CF
又∵∠DFE=∠CFG
∴ΔDFE≌ΔCFG(AAS)
∴FE=FG
∵AD∥BC,BE⊥AD
∴BE⊥CD
∴∠EBG=90°
在RtΔEBG中,F为BG中点
∴BF=![]() EG=EF
EG=EF
∴ΔBEF为等腰三角形。

 名校课堂系列答案
名校课堂系列答案【题目】某水果经销商上月份销售一种新上市的水果,平均售价为10元/千克,月销售量为1000千克.经市场调查,若将该种水果价格调低至x元/千克,则本月份销售量y(千克)与x(元/千克)之间符合一次函数关系,并且得到了表中的数据:
价格x(元/千克) | 7 | 5 |
价格y(千克) | 2000 | 4000 |
(1)求y与x之间的函数解析式;
(2)已知该种水果上月份的成本价为5元/千克,本月份的成本价为4元/千克,要使本月份销售该种水果所获利润比上月份增加20%,同时又要让顾客得到实惠,那么该种水果价格每千克应调低至多少元?