题目内容
检验下列方程后面括号内所列各数是否为相应方程的解:
(1)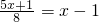 ;
;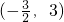
(2)2(y-2)-9(1-y)=3(4y-1).(-10,10)
解:(1)把x=- 代入原方程;
代入原方程;
左边= =-
=- ,
,
右边=- -1=-
-1=- .
.
∵左边≠右边,
∴x=- 不是该方程的解.
不是该方程的解.
把x=3代入方程,得
左边= =2,
=2,
右边=3-1=2.
∵左边=右边,
∴x=3是该方程的解;
(2)把y=-10代入原方程.
左边=2(-10-2)-9(1+10)=-123,右边=3×[4×(-10)-1]=-123,
∵左边=右边,
∴y=-10是原方程的解;
把y=10代入原方程.
左边=2(10-2)-9(1-10)=97,右边=3×(4×10-1)=117,
∵左边≠右边,
∴y=10不是原方程的解.
分析:方程的解就是能够使方程两边左右相等的未知数的值,即利用方程的解代替方程中的未知数,所得到的式子左右两边相等.所以把括号内的数分别代入已知方程,进行一一验证.
点评:本题考查了方程的解的定义.此题是利用代入法进行验证的.
 代入原方程;
代入原方程;左边=
 =-
=- ,
,右边=-
 -1=-
-1=- .
.∵左边≠右边,
∴x=-
 不是该方程的解.
不是该方程的解.把x=3代入方程,得
左边=
 =2,
=2,右边=3-1=2.
∵左边=右边,
∴x=3是该方程的解;
(2)把y=-10代入原方程.
左边=2(-10-2)-9(1+10)=-123,右边=3×[4×(-10)-1]=-123,
∵左边=右边,
∴y=-10是原方程的解;
把y=10代入原方程.
左边=2(10-2)-9(1-10)=97,右边=3×(4×10-1)=117,
∵左边≠右边,
∴y=10不是原方程的解.
分析:方程的解就是能够使方程两边左右相等的未知数的值,即利用方程的解代替方程中的未知数,所得到的式子左右两边相等.所以把括号内的数分别代入已知方程,进行一一验证.
点评:本题考查了方程的解的定义.此题是利用代入法进行验证的.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目