题目内容
如图，已知梯形ABCD，AD∥BC，AF交CD于E，交BC的延长线于F．
（1）若∠B+∠DCF=180°，求证：四边形ABCD是等腰梯形；
（2）若E是线段CD的中点，且CF：CB=1：3，AD=6，求梯形ABCD中位线的长．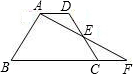
（1）若∠B+∠DCF=180°，求证：四边形ABCD是等腰梯形；
（2）若E是线段CD的中点，且CF：CB=1：3，AD=6，求梯形ABCD中位线的长．
（1）证明：∵∠DCB+∠DCF=180°，
又∵∠B+∠DCF=180°，
∴∠B=∠DCB．
∵四边形ABCD是梯形，
∴四边形ABCD是等腰梯形．
（2）∵AD∥BC，
∴∠DAE=∠F．
∵E是线段CD的中点，
∴DE=CE．
又∵∠DEA=∠FEC，
∴△ADE≌△FCE，
∴AD=CF，
∵CF：BC=1：3，
∴AD：BC=1：3．
∵AD=6，
∴BC=18．
∴梯形ABCD的中位线=（18+6）÷2=12．
又∵∠B+∠DCF=180°，
∴∠B=∠DCB．
∵四边形ABCD是梯形，
∴四边形ABCD是等腰梯形．
（2）∵AD∥BC，
∴∠DAE=∠F．
∵E是线段CD的中点，
∴DE=CE．
又∵∠DEA=∠FEC，
∴△ADE≌△FCE，
∴AD=CF，
∵CF：BC=1：3，
∴AD：BC=1：3．
∵AD=6，
∴BC=18．
∴梯形ABCD的中位线=（18+6）÷2=12．
练习册系列答案
相关题目
9、如图，已知梯形ABCD中，AD∥BC，BE平分∠ABC，BE⊥CD，∠A=110°，AD=3，AB=5，则BC的长为（ ）
点到达终点时，另一点也随之停止．过Q作QD∥AB交AC于点D，连接PD，设运动时间为t秒时，四边形BQDP的面积为s．
（2007•遂宁）如图，已知等腰△ABC的面积为4cm2，点D、E分别是AB、AC边的中点，则梯形DBCE的面积为