题目内容
【题目】如图,抛物线![]() 的开口向下,与x轴交于点A(﹣3,0)和点B(1,0).与y轴交于点C,顶点为D.
的开口向下,与x轴交于点A(﹣3,0)和点B(1,0).与y轴交于点C,顶点为D.
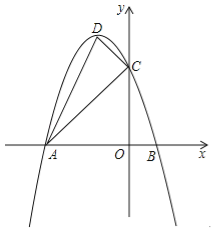
(1)求顶点D的坐标.(用含a的代数式表示);
(2)若△ACD的面积为3.
①求抛物线的解析式;
②将抛物线向右平移,使得平移后的抛物线与原抛物线交于点P,且∠PAB=∠DAC,求平移后抛物线的解析式.
【答案】(1)D(﹣1,﹣4a);(2)①![]() ,②
,②![]() 或
或![]()
【解析】
试题分析:
(1)已知抛物线与x轴的两交点的横坐标分别是﹣3和1,设抛物线解析式的交点式![]() ,再配方为顶点式,可确定顶点坐标。
,再配方为顶点式,可确定顶点坐标。
(2)①设AC与抛物线对称轴的交点为E,先运用待定系数法求出直线AC的解析式,求出点E的坐标,即可得到DE的长,然后由S△ACD=![]() ×DE×OA列出方程,解方程求出a的值,即可确定抛物线的解析式.
×DE×OA列出方程,解方程求出a的值,即可确定抛物线的解析式.
②先运用勾股定理的逆定理判断出在△ACD中∠ACD=90°,利用三角函数求出tan∠DAC=![]() .设抛物线向右平移后的抛物线解析式为
.设抛物线向右平移后的抛物线解析式为![]() ,两条抛物线交于点P,直线AP与y轴交于点F.根据正切函数的定义求出OF=1.分两种情况进行讨论:
,两条抛物线交于点P,直线AP与y轴交于点F.根据正切函数的定义求出OF=1.分两种情况进行讨论:
(Ⅰ)如图2①,F点的坐标为(0,1),(Ⅱ)如图2②,F点的坐标为(0,﹣1).
针对这两种情况,都可以先求出点P的坐标,再得出m的值,进而求出平移后抛物线的解析式.
试题解析:
解:(1)∵抛物线![]() 与x轴交于点A(﹣3,0)和点B(1,0),
与x轴交于点A(﹣3,0)和点B(1,0),
∴抛物线解析式为![]() ,
,
∵![]() ,
,
∴顶点D的坐标为(﹣1,﹣4a).
(2)①如图1,设AC与抛物线对称轴的交点为E,
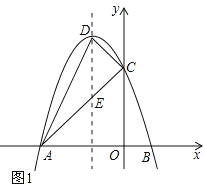
∵抛物线![]() 与y轴交于点C,
与y轴交于点C,
∴C点坐标为(0,﹣3a).
设直线AC的解析式为:![]() ,
,
则:![]() ,解得:
,解得:![]() .
.
∴直线AC的解析式为:![]() .
.
∴点E的坐标为:(﹣1,﹣2a).∴DE=﹣4a﹣(﹣2a)=﹣2a.
∴![]() .
.
∴﹣3a=3,解得a=﹣1.
∴抛物线的解析式为![]() .
.
②∵![]() ,∴顶点D的坐标为(﹣1,4),C(0,3).
,∴顶点D的坐标为(﹣1,4),C(0,3).
∵A(﹣3,0),
∴AD2=(﹣1+3)2+(4﹣0)2=20,CD2=(﹣1﹣0)2+(4﹣3)2=2,
AC2=(0+3)2+(3﹣0)2=18.
∴AD2=CD2+AC2。∴∠ACD=90°.
∴![]() .
.
∵∠PAB=∠DAC,∴tan∠PAB=tan∠DAC=![]() .
.
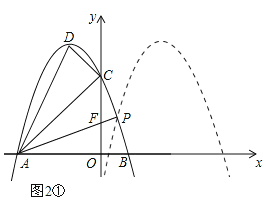
如图2,设![]() 向右平移后的抛物线解析式为
向右平移后的抛物线解析式为![]() ,两条抛物线交于点P,直线AP与y轴交于点F,
,两条抛物线交于点P,直线AP与y轴交于点F,
∵![]() ,
,
∴OF=1,则F点的坐标为(0,1)或(0,﹣1).
分两种情况:
(Ⅰ)如图2①,当F点的坐标为(0,1)时,易求直线AF的解析式为![]() ,
,
由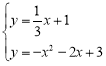 解得,
解得,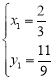 ,
,![]() (舍去).
(舍去).
∴P点坐标为(![]() ,
,![]() )。
)。
将P点坐标(![]() ,
,![]() )代入
)代入![]() ,
,
得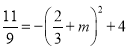 ,解得
,解得![]() ,
,![]() (舍去).
(舍去).
∴平移后抛物线的解析式为![]() .
.
(Ⅱ)如图2②,当F点的坐标为(0,﹣1)时,易求直线AF的解析式为![]() .
.
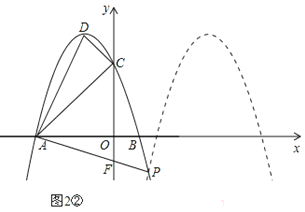
由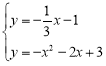 ,解得:
,解得: ,
,![]() (舍去).
(舍去).
∴P点坐标为(![]() ,
,![]() ).
).
将P点坐标(![]() ,
,![]() )代入
)代入![]() ,
,
得![]() ,解得
,解得![]() ,
,![]() (舍去).
(舍去).
∴平移后抛物线的解析式为![]() .
.
综上可知,平移后抛物线的解析式为![]() 或
或![]() .
.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案