题目内容
【题目】如图,过边长为2的等边三角形ABC的顶点C作直线l⊥ BC,然后作△ABC关于直线l对称的△A′B′C,P为线段A′C上一动点,连接AP,PB,则AP+PB的最小值是 ( )
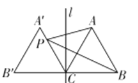
A.4B.3C.2D.2+![]()
【答案】A
【解析】
连接AA′,根据现有条件可推出△A′B′C≌△AA′C,连接AB′交A′C于点E,
易证△A′B′E≌△A′AE,可得点A关于A′C对称的点是B′,可得当点P与点C重合时,AP+PB取最小值,即可求得答案.
解:如图,连接AA′,
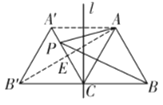
由对称知△ABC,△A′B′C都是等边三角形,
∴∠ACB=∠A′CB′=60°,
∴∠A′CA=60°,
由题意得△ABC≌△A′B′C,
∴AC=A′C,
∴△ACA′是等边三角形,
∴△A′B′C≌△AA′C,
连接AB′交A′C于点E,
易证△A′B′E≌△A′AE,
∴∠A′EB′=∠A′EA=90°,B′E=AE,
∴点A关于A′C对称的点是B′,
∴当点P与点C重合时,AP+PB取最小值,此时AP+PB=AC+BC=2+2=4,
故选:A.

练习册系列答案
相关题目