题目内容
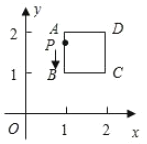
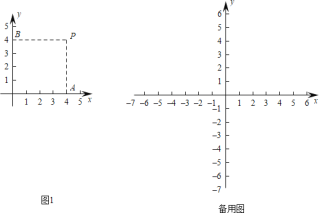
【题目】在平面直角坐标系中,过一点分别作x轴,y轴的垂线,如果由这点、原点及两个垂足为顶点的矩形的周长与面积相等,那么称这个点是平面直角坐标系中的“巧点”.例如,图1中过点P(4,4)分別作x轴,y轴的垂线,垂足为A,B,矩形OAPB的周长为16,面积也为16,周长与面积相等,所以点P是巧点.请根据以上材料回答下列问题:
(1)已知点C(1,3),D(-4,-4),E(5,-![]() ),其中是平面直角坐标系中的巧点的是______;
),其中是平面直角坐标系中的巧点的是______;
(2)已知巧点M(m,10)(m>0)在双曲线y=![]() (k为常数)上,求m,k的值;
(k为常数)上,求m,k的值;
(3)已知点N为巧点,且在直线y=x+3上,求所有满足条件的N点坐标.
【答案】(1)D和E;(2)m=![]() ,k=25;(3)N的坐标为(-6,-3)或(3,6).
,k=25;(3)N的坐标为(-6,-3)或(3,6).
【解析】
(1)利用矩形的周长公式、面积公式结合巧点的定义,即可找出点D,E是巧点;
(2)利用巧点的定义可得出关于m的一元一次方程,解之可得出m的值,再利用反比例函数图象上点的坐标特征,可求出k值;
(3)设N(x,x+3),根据巧点的定义得到2(|x|+|x+3|)=|x||x+3|,分三种情况讨论即可求解.
(1)∵(4+4)×2=4×4,(5+![]() )×2=5×
)×2=5×![]() ,(1+3)×2≠1×3,
,(1+3)×2≠1×3,
∴点D和点E是巧点,
故答案为:D和E;
(2)∵点M(m,10)(m>0),
∴矩形的周长=2(m+10),面积=10m.
∵点M是巧点,
∴2(m+10)=10m,解得:m=![]() ,
,
∴点M(![]() ,10).
,10).
∵点M在双曲线y=![]() 上,
上,
∴k=![]() ×10=25;
×10=25;
(3)设N(x,x+3),则2(|x|+|x+3|)=|x||x+3|,
当x≤-3时,化简得:x2+7x+6=0,解得:x=-6或x=-1(舍去);
当-3<x<0时,化简得:x2+3x+6=0,无实根;
当x≥0时,化简得:x2-x-6=0,解得:x=3或x=-2(舍去),
综上,点N的坐标为(-6,-3)或(3,6).

 阅读快车系列答案
阅读快车系列答案