��Ŀ����
��ͼ����֪����ֱ������ϵ�У���E��O���������1����λ/����ٶ���x���������˶�����F��O���������2����λ/����ٶ���y���������˶���B��4��2������BEΪֱ������O1��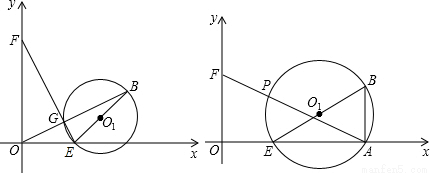
��1������E��Fͬʱ���������߶�EF���߶�OB���ڵ�G�����жϵ�G���O1��λ�ù�ϵ����֤����Ľ��ۣ�
��2���ڣ�1���������£�����FB������ʱFB���O1���У�
��3������E��ǰ2���������F�ٳ���������F������E��A������ʱ����BA��x���ڵ�A������AF����O1�ڵ�P������AP•AF��ֵ�Ƿ�ᷢ���仯�������䣬��˵�����ɲ�����ֵ�����仯��������ֵ�ı仯��Χ��
���𰸡���������1��Ҫ�жϵ�G���O1��λ�ù�ϵ��ֻ��Ƚ�O1G���O1�İ뾶O1B�Ĵ�С�����E����t�룬��E��t��0����F��0��2t�����ô���ϵ�������ֱ��EF��ֱ��OB�Ľ���ʽ��ȷ����G�����꣬�������ľ��빫ʽ�����O1G��O1B�Ĵ�С���Ӷ������ж���
��2�����t��ʱFB���O1���У���ô��FBE=90°����RT��BEF��RT��OEF�У�����EF�����г����̣����t��ֵ��
��3�����F����t�룬��E��t+2��0����F��0��2t������P��x��y������tan��FAO=y����4-x��=2t��4���ó�x=4-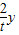 ����P��4-
����P��4-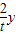 ��y������ΪBEΪֱ�������ԡ�BPE=90°��PE2+BP2=BE2���ó�y��t�Ĺ�ϵ�����Ժ�t�Ĵ���ʽ�ó�P�����꣬�ֱ����AP��AF�ij������ݽ���жϣ�
��y������ΪBEΪֱ�������ԡ�BPE=90°��PE2+BP2=BE2���ó�y��t�Ĺ�ϵ�����Ժ�t�Ĵ���ʽ�ó�P�����꣬�ֱ����AP��AF�ij������ݽ���жϣ�
����⣺��1�����E����t�룬��E��t��0����F��0��2t����
��ֱ��EF�ķ���Ϊy=kx+b����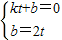 ��
��
����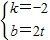 ��
��
��y=-2x+2t��
��ֱ��OB�ķ���Ϊy= x��
x��
�߽ⷽ����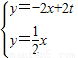 ��
��
��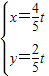 ��
��
��G�� t��
t�� t����
t����
��O1��BE���е㣬
��O1�� ��1����
��1����
��O1G2=��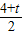 -
- t��2+��1-
t��2+��1- t��2=
t��2= t2-2t+5��O1B2=��4-
t2-2t+5��O1B2=��4-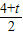 ��2+12=
��2+12= t2-2t+5��
t2-2t+5��
��O1G=O1B����G�ڡ�O1�ϣ�
��2����t��ʱFB���O1���У���ôE��t��0����F��0��2t������FBE=90°��
��EF2=BE2+BF2��EF2=OE2+OF2��
�ࣨ4-t��2+22+42+��2-2t��2=t2+��2t��2��
���t=2.5��
��3�����F����t�룬��E��t+2��0����F��0��2t����
��P��x��y����
��tan��FAO=y����4-x��=2t��4��
��x=4-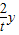 ��
��
��P��4-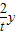 ��y����
��y����
��BEΪֱ����
���BPE=90°��
��PE2+BP2=BE2
�����������ľ��빫ʽ��B��P��E��F������������ã�
��y= ��
��
��x=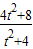 ��
��
��P��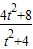 ��
�� ����
����
��AP2=��4-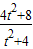 ��2+��
��2+�� ��2��
��2��
��AP=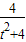 ×
×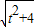 ��AF=
��AF= =2
=2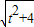 ��
��
��AP•AF=8���Dz��ᷢ���仯�ģ�
�����������ۺϿ��������ߵ��ж������Ǻ�����֪ʶ��������Ҫ����ץס���������ҵ�������ϵ����Ŀ��һ���Ѷȣ����Կ���ѧ�����ۺ�ʵ����
��2�����t��ʱFB���O1���У���ô��FBE=90°����RT��BEF��RT��OEF�У�����EF�����г����̣����t��ֵ��
��3�����F����t�룬��E��t+2��0����F��0��2t������P��x��y������tan��FAO=y����4-x��=2t��4���ó�x=4-
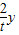 ����P��4-
����P��4-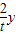 ��y������ΪBEΪֱ�������ԡ�BPE=90°��PE2+BP2=BE2���ó�y��t�Ĺ�ϵ�����Ժ�t�Ĵ���ʽ�ó�P�����꣬�ֱ����AP��AF�ij������ݽ���жϣ�
��y������ΪBEΪֱ�������ԡ�BPE=90°��PE2+BP2=BE2���ó�y��t�Ĺ�ϵ�����Ժ�t�Ĵ���ʽ�ó�P�����꣬�ֱ����AP��AF�ij������ݽ���жϣ�����⣺��1�����E����t�룬��E��t��0����F��0��2t����
��ֱ��EF�ķ���Ϊy=kx+b����
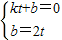 ��
������
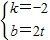 ��
����y=-2x+2t��
��ֱ��OB�ķ���Ϊy=
 x��
x���߽ⷽ����
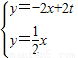 ��
����
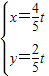 ��
����G��
 t��
t�� t����
t������O1��BE���е㣬
��O1��
 ��1����
��1������O1G2=��
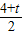 -
- t��2+��1-
t��2+��1- t��2=
t��2= t2-2t+5��O1B2=��4-
t2-2t+5��O1B2=��4-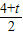 ��2+12=
��2+12= t2-2t+5��
t2-2t+5����O1G=O1B����G�ڡ�O1�ϣ�
��2����t��ʱFB���O1���У���ôE��t��0����F��0��2t������FBE=90°��
��EF2=BE2+BF2��EF2=OE2+OF2��
�ࣨ4-t��2+22+42+��2-2t��2=t2+��2t��2��
���t=2.5��
��3�����F����t�룬��E��t+2��0����F��0��2t����
��P��x��y����
��tan��FAO=y����4-x��=2t��4��
��x=4-
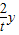 ��
����P��4-
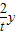 ��y����
��y������BEΪֱ����
���BPE=90°��
��PE2+BP2=BE2
�����������ľ��빫ʽ��B��P��E��F������������ã�
��y=
 ��
����x=
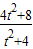 ��
����P��
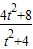 ��
�� ����
������AP2=��4-
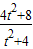 ��2+��
��2+�� ��2��
��2����AP=
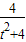 ×
×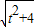 ��AF=
��AF= =2
=2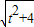 ��
����AP•AF=8���Dz��ᷢ���仯�ģ�
�����������ۺϿ��������ߵ��ж������Ǻ�����֪ʶ��������Ҫ����ץס���������ҵ�������ϵ����Ŀ��һ���Ѷȣ����Կ���ѧ�����ۺ�ʵ����

��ϰ��ϵ�д�
 Ӣ�ŵ��ϵ�д�
Ӣ�ŵ��ϵ�д� ������������Ծ�ϵ�д�
������������Ծ�ϵ�д�
�����Ŀ

 ��ͼ���һ����֧λ�ڵ�һ���ޣ�
��ͼ���һ����֧λ�ڵ�һ���ޣ�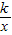 ��ͼ���ͼ���ϣ���k��ֵ��
��ͼ���ͼ���ϣ���k��ֵ�� S1��
S1��
 ��ͼ����y�ύ�ڵ�A��
��ͼ����y�ύ�ڵ�A�� ��ͼ��ֱ��ڵ�M��N����֪��AOB�����Ϊ1����M������
��ͼ��ֱ��ڵ�M��N����֪��AOB�����Ϊ1����M������ ʱx��ȡֵ��Χ��
ʱx��ȡֵ��Χ��
 �У��ı���OABC�Ǿ��Σ���A��C����
�У��ı���OABC�Ǿ��Σ���A��C���� ����
���� ��
�� ������O��A��B�ڵ�E��
������O��A��B�ڵ�E��
