题目内容
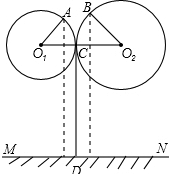
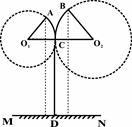
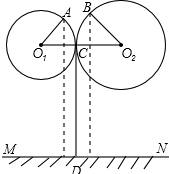 某街道两旁正在安装漂亮的路灯,经查看路灯图纸,小红发现该路灯的设计可以看作是“相切两圆”的一部分,部分数据如图所示:⊙O1、⊙O2相切于点C,CD切⊙O1于点C,A、B为路灯灯泡.已知∠AO1O2=∠BO2O1=60°.A、B、C三点距地面MN的距离分别为
某街道两旁正在安装漂亮的路灯,经查看路灯图纸,小红发现该路灯的设计可以看作是“相切两圆”的一部分,部分数据如图所示:⊙O1、⊙O2相切于点C,CD切⊙O1于点C,A、B为路灯灯泡.已知∠AO1O2=∠BO2O1=60°.A、B、C三点距地面MN的距离分别为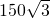 cm,
cm,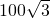 cm,
cm,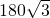 cm,请根据以上图文信息,求:
cm,请根据以上图文信息,求:
(1)⊙O1、⊙O2的半径分别多少cm?
(2)把A、B两个灯泡看作两个点,求线段AB的长.
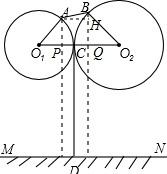 解:(1)过点A作AP⊥MN交O1O2于点P,
解:(1)过点A作AP⊥MN交O1O2于点P,∵A、B、C三点距地面MN的距离分别为
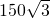 cm,
cm,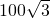 cm,
cm,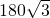 cm,
cm,∴AP=150
 -100
-100 =50
=50 (cm),
(cm),∴在Rt△O1AP中,O1A=
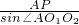 =
=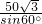 =100(cm),
=100(cm),同理:O1B=
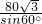 =160(cm),
=160(cm),∴⊙O1、⊙O2的半径分别为100cm和160cm.
(2)如图,过点A作AP⊥MN交O1O2于点P,过点B作BQ⊥MN交O1O2于点Q,过点A作AH⊥BQ于点H,
则四边形APQH是矩形,
∵O1P=
 O1A,O2Q=
O1A,O2Q= O2B,
O2B,∴AH=PQ=
 (100+160)=130(cm),BH=180
(100+160)=130(cm),BH=180 -150
-150 =30
=30 (cm),
(cm),∴AB=
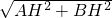 =
=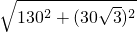 =140(cm).
=140(cm).即线段AB的长为140cm.
分析:(1)首先过点A作AP⊥MN交O1O2于点P,由A、B、C三点距地面MN的距离分别为
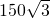 cm,
cm,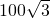 cm,
cm,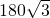 cm,可求得AP的长,然后由三角函数的性质,求得O1A的长,同理可求得⊙O2的半径;
cm,可求得AP的长,然后由三角函数的性质,求得O1A的长,同理可求得⊙O2的半径;(2)首先过点A作AP⊥MN交O1O2于点P,过点B作BQ⊥MN交O1O2于点Q,过点A作AH⊥BQ于点H,可求得AH与BH的长,然后由勾股定理求得线段AB的长.
点评:此题考查了相切两圆的性质、勾股定理以及三角函数的性质.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
 某街道两旁正在安装漂亮的路灯,经查看路灯图纸,小红发现该路灯的设计可以看作是“相切两圆”的一部分,部分数据如图所示:⊙O1、⊙O2相切于点C,CD切⊙O1于点C,A、B为路灯灯泡.已知∠AO1O2=∠BO2O1=60°.A、B、C三点距地面MN的距离分别为
某街道两旁正在安装漂亮的路灯,经查看路灯图纸,小红发现该路灯的设计可以看作是“相切两圆”的一部分,部分数据如图所示:⊙O1、⊙O2相切于点C,CD切⊙O1于点C,A、B为路灯灯泡.已知∠AO1O2=∠BO2O1=60°.A、B、C三点距地面MN的距离分别为 )
)
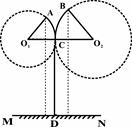
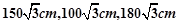 ,请根据以上图文信息,求:
,请根据以上图文信息,求:
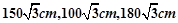 ,请根据以上图文信息,求:
,请根据以上图文信息,求: