题目内容
如图,正方形ABCD的边长为5cm,动点P从点C出发,沿折线C-B-A-D向终点D运动,速度为acm/s;动点Q从点B出发,沿对角线BD向终点D运动,速度为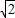 cm/s.当其中一点到达自己的终点时,另一点也停止运动.当点P、点Q同时从各自的
cm/s.当其中一点到达自己的终点时,另一点也停止运动.当点P、点Q同时从各自的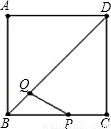 起点运动时,以PQ为直径的⊙O与直线BD的位置关系也随之变化,设运动时间为t(s).
起点运动时,以PQ为直径的⊙O与直线BD的位置关系也随之变化,设运动时间为t(s).(1)写出在运动过程中,⊙O与直线BD所有可能的位置关系______;
(2)在运动过程中,若a=3,求⊙O与直线BD相切时t的值;
(3)探究:在整个运动过程中,是否存在正整数a,使得⊙O与直线BD相切两次?若存在,请直接写出符合条件的两个正整数a及相应的t的值;若不存在,请说明理由.
【答案】分析:(1)因为直径PQ与直线BD有一个交点,直线与圆不可能相离;
(2)运动过程中,已知∠PBQ=45°,直线与圆相切时,PQ⊥BD,围绕等腰直角三角形的两边关系,建立方程求解;
(3)根据题目的限制条件t<5,根据(2)得出一般结论,再根据限制条件求a的范围.
解答:解:(1)点Q为直线BD上的点,PQ为直径,⊙O与直线BD的位置关系只可能是:相切、相交;
(2)当P点在BC上时,PQ⊥BD,⊙O与直线BD相切,
△BQP为等腰直角三角形,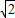 BQ=PB,即
BQ=PB,即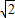 ×
×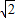 t=5-3t,
t=5-3t,
解得t1=1,
当P点在AB上时,PQ⊥BD,⊙O与直线BD相切,
△BQP为等腰直角三角形, BQ=PB,即
BQ=PB,即 ×
×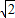 t=3t-5,
t=3t-5,
解得t2=5(舍去),
当P点在AD上时,PQ⊥BD,⊙O与直线BD相切,
△BQP为等腰直角三角形,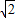 BQ=PB,即2t=15-3t,
BQ=PB,即2t=15-3t,
t3=3(舍去);
故t=1时,⊙O与直线BD相切.
(3)存在,由(2)可知,(a+2)t=5,或者(a-2)t=5,
且t<5,故a≥4且a为正整数,t1=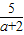 ,t2=
,t2=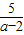 .
.
点评:本题考查了运动过程中,满足条件时,△BPQ始终是等腰直角三角形这一条件.
(2)运动过程中,已知∠PBQ=45°,直线与圆相切时,PQ⊥BD,围绕等腰直角三角形的两边关系,建立方程求解;
(3)根据题目的限制条件t<5,根据(2)得出一般结论,再根据限制条件求a的范围.
解答:解:(1)点Q为直线BD上的点,PQ为直径,⊙O与直线BD的位置关系只可能是:相切、相交;
(2)当P点在BC上时,PQ⊥BD,⊙O与直线BD相切,
△BQP为等腰直角三角形,
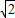 BQ=PB,即
BQ=PB,即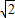 ×
×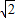 t=5-3t,
t=5-3t,解得t1=1,
当P点在AB上时,PQ⊥BD,⊙O与直线BD相切,
△BQP为等腰直角三角形,
 BQ=PB,即
BQ=PB,即 ×
×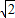 t=3t-5,
t=3t-5,解得t2=5(舍去),
当P点在AD上时,PQ⊥BD,⊙O与直线BD相切,
△BQP为等腰直角三角形,
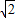 BQ=PB,即2t=15-3t,
BQ=PB,即2t=15-3t,t3=3(舍去);
故t=1时,⊙O与直线BD相切.
(3)存在,由(2)可知,(a+2)t=5,或者(a-2)t=5,
且t<5,故a≥4且a为正整数,t1=
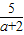 ,t2=
,t2=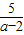 .
.点评:本题考查了运动过程中,满足条件时,△BPQ始终是等腰直角三角形这一条件.

练习册系列答案
相关题目
 19、如图:正方形ABCD,M是线段BC上一点,且不与B、C重合,AE⊥DM于E,CF⊥DM于F.求证:AE2+CF2=AD2.
19、如图:正方形ABCD,M是线段BC上一点,且不与B、C重合,AE⊥DM于E,CF⊥DM于F.求证:AE2+CF2=AD2. 如图,正方形ABCD中,E点在BC上,AE平分∠BAC.若BE=
如图,正方形ABCD中,E点在BC上,AE平分∠BAC.若BE= 如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.下列结论:①△ABG≌△AFG;②BG=GC;③AG∥CF;④S△FGC=3.其中正确结论的个数是( )
如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.下列结论:①△ABG≌△AFG;②BG=GC;③AG∥CF;④S△FGC=3.其中正确结论的个数是( ) 17、如图,正方形ABCD的边长为4,将一个足够大的直角三角板的直角顶点放于点A处,该三角板的两条直角边与CD交于点F,与CB延长线交于点E,四边形AECF的面积是
17、如图,正方形ABCD的边长为4,将一个足够大的直角三角板的直角顶点放于点A处,该三角板的两条直角边与CD交于点F,与CB延长线交于点E,四边形AECF的面积是 如图,正方形ABCD的边CD在正方形ECGF的边CE上,连接BE、DG.
如图,正方形ABCD的边CD在正方形ECGF的边CE上,连接BE、DG.