题目内容
以坐标原点为圆心,1为半径的圆分别交x,y轴的正半轴于点A,B。
(1)如图一,动点P从点A处出发,沿x轴向右匀速运动,与此同时,动点Q从点B处出发,沿圆周按顺时针方向匀速运动,若点Q的运动速度比点P的运动速度慢,经过1秒后点P运动到点(2,0),此时PQ恰好是 的切线,连接OQ,求∠QOP的大小;
的切线,连接OQ,求∠QOP的大小;
(1)如图一,动点P从点A处出发,沿x轴向右匀速运动,与此同时,动点Q从点B处出发,沿圆周按顺时针方向匀速运动,若点Q的运动速度比点P的运动速度慢,经过1秒后点P运动到点(2,0),此时PQ恰好是
 的切线,连接OQ,求∠QOP的大小;
的切线,连接OQ,求∠QOP的大小;
(2)若点Q按照(1)中的方向和速度继续运动,点P停留在点(2,0)处不动,求点Q再经过5秒后直线PQ被 截得的弦长。
截得的弦长。
 截得的弦长。
截得的弦长。
图二(备用图)
| 解:(1)如图一,连结AQ, 由题意可知:OQ=OA=1, ∵OP=2, ∴A为OP的中点, ∵PQ与  相切于点Q, 相切于点Q,∴  为直角三角形, 为直角三角形,∴  , ,即ΔOAQ为等边三角形, ∴∠QOP=60°; |
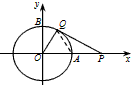 图一 |
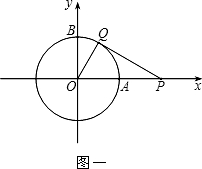
(2)由(1)可知点Q运动1秒时经过的弧长所对的圆心角为30°,若Q按照(1)中的方向和速度继续运动,那么再过5秒,则Q点落在 与y轴负半轴的交点处(如图二), 与y轴负半轴的交点处(如图二),设直线PQ与  的另外一个交点为D,过O作OC⊥QD于点C,则C为QD的中点, 的另外一个交点为D,过O作OC⊥QD于点C,则C为QD的中点,∵∠QOP=90°,OQ=1,OP=2, ∴QP=  , ,∵  , ,∴OC=  , ,∵OC⊥QD,OQ=1,OC=  , ,∴QC=  , ,∴QD=  。 。 |
 |

练习册系列答案
相关题目

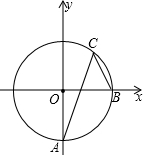 如图,以坐标原点为圆心的⊙O交y轴的负半轴于点A,交x轴的正半轴于点B,C为⊙O位于第一象限部分上的任一点,则∠ACB=
如图,以坐标原点为圆心的⊙O交y轴的负半轴于点A,交x轴的正半轴于点B,C为⊙O位于第一象限部分上的任一点,则∠ACB=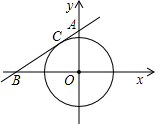 径的圆相切于点C,且与x轴的负半轴相交于点B.
径的圆相切于点C,且与x轴的负半轴相交于点B. (2012•昆山市二模)如图,直线l的解析式为
(2012•昆山市二模)如图,直线l的解析式为 如图,点P(x,y)在以坐标原点为圆心、5为半径的圆上,若x,y都是整数,请探究这样的点P一共有多少个?写出这些点的坐标.
如图,点P(x,y)在以坐标原点为圆心、5为半径的圆上,若x,y都是整数,请探究这样的点P一共有多少个?写出这些点的坐标.