题目内容
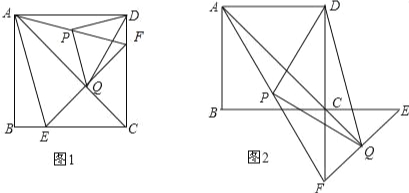
【题目】如图1，已知一次函数y=x+3的图象与x轴、y轴分别交于A、B两点，抛物线y=﹣x2+bx+c过A、B两点，且与x轴交于另一点C．
（1）求b、c的值；
（2）如图1，点D为AC的中点，点E在线段BD上，且BE=2ED，连接CE并延长交抛物线于点M，求点M的坐标；
（3）将直线AB绕点A按逆时针方向旋转15°后交y轴于点G，连接CG，如图2，P为△ACG内一点，连接PA、PC、PG，分别以AP、AG为边，在他们的左侧作等边△APR，等边△AGQ，连接QR
①求证：PG=RQ；
②求PA+PC+PG的最小值，并求出当PA+PC+PG取得最小值时点P的坐标．
【答案】（1）b=﹣2，c=3（2）（﹣
，
）（3）①证明见解析②（﹣
，
）
【解析】
试题分析：（1）把A（﹣3，0），B（0，3）代入抛物线y=﹣x2+bx+c即可解决问题．
（2）首先求出A、C、D坐标，根据BE=2ED，求出点E坐标，求出直线CE，利用方程组求交点坐标M．
（3）①欲证明PG=QR，只要证明△QAR≌△GAP即可．②当Q、R、P、C共线时，PA+PG+PC最小，作QN⊥OA于N，AM⊥QC于M，PK⊥OA于K，由sin∠ACM=
求出AM，CM，利用等边三角形性质求出AP、PM、PC，由此即可解决问题．
试题解析：（1）∵一次函数y=x+3的图象与x轴、y轴分别交于A、B两点，
∴A（﹣3，0），B（0，3），
∵抛物线y=﹣x2+bx+c过A、B两点，
∴
解得
，
∴b=﹣2，c=3．
（2），对于抛物线y=﹣x2﹣2x+3，令y=0，则﹣x2﹣2x+3=0，解得x=﹣3或1，
∴点C坐标（1，0），
∵AD=DC=2，
∴点D坐标（﹣1，0），
∵BE=2ED，
∴点E坐标（﹣
，1），
设直线CE为y=kx+b，把E、C代入得到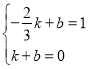
解得
，
∴直线CE为y=﹣
x+
，
由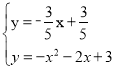
解得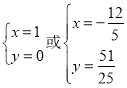
，
∴点M坐标（﹣
，
）．
（3）①∵△AGQ，△APR是等边三角形，
∴AP=AR，AQ=AG，∠QAC=∠RAP=60°，
∴∠QAR=∠GAP，
在△QAR和△GAP中，
，
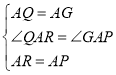∴△QAR≌△GAP，
∴QR=PG．
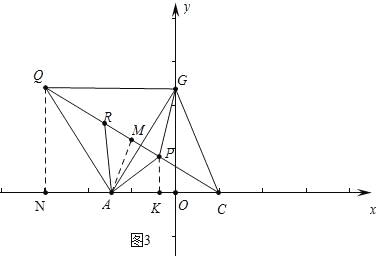
②如图3中，∵PA+PB+PC=QR+PR+PC=QC，
∴当Q、R、P、C共线时，PA+PG+PC最小，
作QN⊥OA于N，AM⊥QC于M，PK⊥OA于K．
∵∠GAO=60°，AO=3，
∴AG=QG=AQ=6，∠AGO=30°，
∵∠QGA=60°，
∴∠QGO=90°，
∴点Q坐标（﹣6，3
），
在RT△QCN中，QN=3，CN=7，∠QNC=90°，
∴QC=
，
∵sin∠ACM=
，
∴AM=
，
∵△APR是等边三角形，
∴∠APM=60°，∵PM=PR，cos30°=
，
∴AP=
，PM=RM=
∴MC=
=
，
∴PC=CM﹣PM=
，
∵
，
∴CK=
，PK=
，
∴OK=CK﹣CO=
，
∴点P坐标（﹣
，
）．
∴PA+PC+PG的最小值为2
，此时点P的坐标（﹣
，
）．
