题目内容
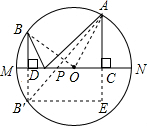
如图，MN为⊙O的直径，A、B是⊙O上的两点，过A作AC⊥MN于点C，过B作BD⊥MN于点D，P为DC上的任意一点，若MN=20，AC=8，BD=6，则PA+PB的最小值是______．
∵MN=20，
∴⊙O的半径=10，
连接OA、OB，
在Rt△OBD中，OB=10，BD=6，
∴OD=
=
=8；
同理，在Rt△AOC中，OA=10，AC=8，
∴OC=
=
=6，
∴CD=8+6=14，
作点B关于MN的对称点B′，连接AB′，则AB′即为PA+PB的最小值，B′D=BD=6，过点B′作AC的垂线，交AC的延长线于点E，
在Rt△AB′E中，
∵AE=AC+CE=8+6=14，B′E=CD=14，
∴AB′=
=
=14
．
故答案为：14
．
∴⊙O的半径=10，
连接OA、OB，
在Rt△OBD中，OB=10，BD=6，
∴OD=
| OB2-BD2 |
| 102-62 |
同理，在Rt△AOC中，OA=10，AC=8，
∴OC=
| OA2-AC2 |
| 102-82 |
∴CD=8+6=14，
作点B关于MN的对称点B′，连接AB′，则AB′即为PA+PB的最小值，B′D=BD=6，过点B′作AC的垂线，交AC的延长线于点E，
在Rt△AB′E中，
∵AE=AC+CE=8+6=14，B′E=CD=14，
∴AB′=
| AE2+B′E2 |
| 142+142 |
| 2 |
故答案为：14
| 2 |
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
