题目内容
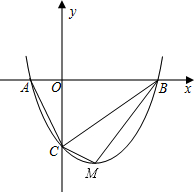 如图,抛物线y=mx2-2mx-3m(m>0)与x轴交于A、B两点,与y轴交于C点.
如图,抛物线y=mx2-2mx-3m(m>0)与x轴交于A、B两点,与y轴交于C点.(1)请求出抛物线顶点M的坐标(用含m的代数式表示),A、B两点的坐标;
(2)经探究可知,△BCM与△ABC的面积比不变,试求出这个比值;
(3)是否存在使△BCM为直角三角形的抛物线?若存在,请求出;如果不存在,请说明理由.
分析:(1)将抛物线的解析式化为顶点坐标式,即可得到顶点M的坐标;抛物线的解析式中,令y=0,可求得A、B的坐标.
(2)易求得C点坐标,即可得到OC的长,以AB为底,OC为高,即可求出△ABC的面积;△BCM的面积无法直接求得,可用割补法求解,过M作MD⊥x轴于D,根据B、C、M四点坐标,可分别求出梯形OCMD、△BDM的面积,它们的面积和减去△BOC的面积即为△BCM的面积,进而可得到△ABC、△BCM的面积比.
(3)首先根据B、C、M的坐标,求出BC2、BM2、CM2的值,由于△BCM中,B、C、M都有可能是直角顶点,所以要分三种情况讨论:①∠BCM=90°,②∠BMC=90°,③∠MBC=90°,在上述三种不同的直角三角形中,利用勾股定理可求得m的值,进而可确定抛物线的解析式.
(2)易求得C点坐标,即可得到OC的长,以AB为底,OC为高,即可求出△ABC的面积;△BCM的面积无法直接求得,可用割补法求解,过M作MD⊥x轴于D,根据B、C、M四点坐标,可分别求出梯形OCMD、△BDM的面积,它们的面积和减去△BOC的面积即为△BCM的面积,进而可得到△ABC、△BCM的面积比.
(3)首先根据B、C、M的坐标,求出BC2、BM2、CM2的值,由于△BCM中,B、C、M都有可能是直角顶点,所以要分三种情况讨论:①∠BCM=90°,②∠BMC=90°,③∠MBC=90°,在上述三种不同的直角三角形中,利用勾股定理可求得m的值,进而可确定抛物线的解析式.
解答:解:(1)∵y=mx2-2mx-3m=m(x2-2x-3)=m(x-1)2-4m,
∴抛物线顶点M的坐标为(1,-4m);(2分)
∵抛物线y=mx2-2mx-3m(m>0)与x轴交于A、B两点,
∴当y=0时,mx2-2mx-3m=0,
∵m>0,
∴x2-2x-3=0;
解得x1=-1,x2=3,
∴A、B两点的坐标为(-1,0)、(3,0).(4分)
(2)当x=0时,y=-3m,
∴点C的坐标为(0,-3m).
∴S△ABC=
×|3-(-1)|×|-3m|=6|m|=6m.(5分)
过点M作MD⊥x轴于点D,则OD=1,BD=OB-OD=2,
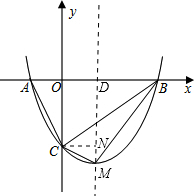 MD=|-4m|=4m.
MD=|-4m|=4m.
∴S△BCM=S△BDM+S梯形OCMD-S△OBC
=
BD?DM+
(OC+OM)?OD-
OB?OC
=
×2×4m+
(3m+4m)×1-
×3×3m
=3m.(7分)
∴S△BCM:S△ABC=1:2,(8分)
故答案为:
;
(3)存在使△BCM为直角三角形的抛物线;
过点C作CN⊥DM于点N,则△CMN为Rt△,CN=OD=1,DN=OC=3m,
∴MN=DM-DN=m.
∴CM2=CN2+MN2=1+m2;
在Rt△OBC中,BC2=OB2+OC2=9+9m2,
在Rt△BDM中,BM2=BD2+DM2=4+16m2;
①如果△BCM是Rt△,且∠BMC=90°,那么CM2+BM2=BC2,
即1+m2+4+16m2=9+9m2,
解得m=±
,
∵m>0,∴m=
.
∴存在抛物线y=
x2-
x-
使得△BCM是Rt△;(10分)
②如果△BCM是Rt△,且∠BCM=90°,那么BC2+CM2=BM2,
即9+9m2+1+m2=4+16m2,
解得m=±1,
∵m>0,
∴m=1;
∴存在抛物线y=x2-2x-3,使得△BCM是Rt△;
③如果△BCM是Rt△,且∠CBM=90°,那么BC2+BM2=CM2,
即9+9m2+4+16m2=1+m2,整理得m2=-
,此方程无解;
∴以∠CBM为直角的直角三角形不存在;
综上所述,存在抛物线y=
x2-
x-
和y=x2-2x-3,使得△BCM是Rt△.(12分)
∴抛物线顶点M的坐标为(1,-4m);(2分)
∵抛物线y=mx2-2mx-3m(m>0)与x轴交于A、B两点,
∴当y=0时,mx2-2mx-3m=0,
∵m>0,
∴x2-2x-3=0;
解得x1=-1,x2=3,
∴A、B两点的坐标为(-1,0)、(3,0).(4分)
(2)当x=0时,y=-3m,
∴点C的坐标为(0,-3m).
∴S△ABC=
| 1 |
| 2 |
过点M作MD⊥x轴于点D,则OD=1,BD=OB-OD=2,
 MD=|-4m|=4m.
MD=|-4m|=4m.∴S△BCM=S△BDM+S梯形OCMD-S△OBC
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=3m.(7分)
∴S△BCM:S△ABC=1:2,(8分)
故答案为:
| 1 |
| 2 |
(3)存在使△BCM为直角三角形的抛物线;
过点C作CN⊥DM于点N,则△CMN为Rt△,CN=OD=1,DN=OC=3m,
∴MN=DM-DN=m.
∴CM2=CN2+MN2=1+m2;
在Rt△OBC中,BC2=OB2+OC2=9+9m2,
在Rt△BDM中,BM2=BD2+DM2=4+16m2;
①如果△BCM是Rt△,且∠BMC=90°,那么CM2+BM2=BC2,
即1+m2+4+16m2=9+9m2,
解得m=±
| ||
| 2 |
∵m>0,∴m=
| ||
| 2 |
∴存在抛物线y=
| ||
| 2 |
| 2 |
3
| ||
| 2 |
②如果△BCM是Rt△,且∠BCM=90°,那么BC2+CM2=BM2,
即9+9m2+1+m2=4+16m2,
解得m=±1,
∵m>0,
∴m=1;
∴存在抛物线y=x2-2x-3,使得△BCM是Rt△;
③如果△BCM是Rt△,且∠CBM=90°,那么BC2+BM2=CM2,
即9+9m2+4+16m2=1+m2,整理得m2=-
| 1 |
| 2 |
∴以∠CBM为直角的直角三角形不存在;
综上所述,存在抛物线y=
| ||
| 2 |
| 2 |
3
| ||
| 2 |
点评:此题考查了二次函数图象与坐标轴交点坐标的求法、图形面积的求法、勾股定理、直角三角形的判定等知识;需要注意的是(3)题中,由于直角三角形的直角顶点不确定,一定要分类讨论,以免漏解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,抛物线y=-x2+mx过点A(4,0),O为坐标原点,Q是抛物线的顶点.
如图,抛物线y=-x2+mx过点A(4,0),O为坐标原点,Q是抛物线的顶点.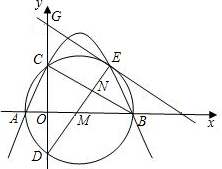 已知:如图,抛物线
已知:如图,抛物线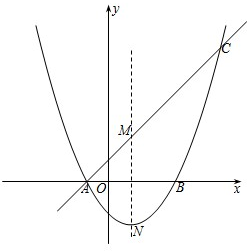 如图,抛物线y=
如图,抛物线y=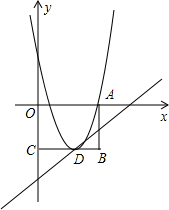 (2010•海沧区质检)如图,抛物线y=x2+bx+c与x轴的右交点为A,顶点D在矩形OABC的边BC上,当y≤0时,x的取值范围是1≤x≤5.
(2010•海沧区质检)如图,抛物线y=x2+bx+c与x轴的右交点为A,顶点D在矩形OABC的边BC上,当y≤0时,x的取值范围是1≤x≤5.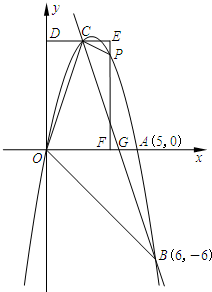 如图,抛物线y=ax2+bx+c经过点A(5,0)、B(6,-6)和原点O,过点B的直线y=mx+n与抛物线相交于点C(2,y).过点C作平行于x轴的直线交y轴于点D,在抛物线对称轴右侧位于直线DC下方的抛物线上,任取一点P,过点P作直线PF平行于y轴,交直线DC于点E,交x轴于点F.
如图,抛物线y=ax2+bx+c经过点A(5,0)、B(6,-6)和原点O,过点B的直线y=mx+n与抛物线相交于点C(2,y).过点C作平行于x轴的直线交y轴于点D,在抛物线对称轴右侧位于直线DC下方的抛物线上,任取一点P,过点P作直线PF平行于y轴,交直线DC于点E,交x轴于点F.