题目内容
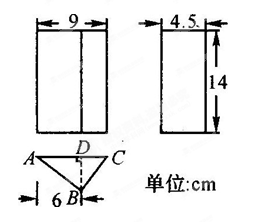
如图，点C为线段AB上一点， AC︰CB＝3︰2，D、E两点分别为AC、AB的中点，若线段DE＝2cm，则AB的长为 （ ）
A.8 cm B.12 cm C.14 cm D. 10 cm
D．
解析试题分析：依据各线段间的比例关系，列方程求解即可.
设AB=
，则AC=
，BC=
，
∵D、E两点分别为AC、AB的中点，
∴DC=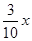
，BE=
，
∵DE=DC-EC=DC-（BE-BC），
∴
，
解得：x=10，
则AB的长为10cm，故选D.
考点：两点间距离．
练习册系列答案
阶梯计算系列答案
相关题目
如图，小聪把一块含有60°角的直角三角板的两个顶点放在直尺的对边上，并测得∠1=23°，则∠2的度数是（ ）
| A．23° | B．22° | C．37° | D．67° |
下列语句不是命题的是( )
| A．对顶角相等 | B．连结AB并延长至C点 |
| C．内错角相等 | D．同角的余角相等 |
CD,垂足为O.若
，则
的大小为
下列说法中正确的是（ ）
| A．对顶角不一定相等 |
| B．有公共顶点且相等的两个角是对顶角 |
| C．对顶角的补角相等 |
| D．两直线相交所成的角是对顶角 |
如图，有一块含有45°角的直角三角板的两个顶点放在直尺的对边上．如果∠1＝20°，那么∠2的度数是( )
| A．30° | B．25° | C．20° | D．15° |
如图，由AB∥CD，可以得到（ ）
| A．∠1=∠2 | B．∠2=∠3 | C．∠1=∠4 | D．∠3=∠4 |
