题目内容
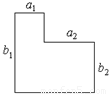
(2005•舟山)挪威数学家阿贝尔,年轻时就利用阶梯形,发现了一个重要的恒等式--阿贝尔公式:如图是一个简单的阶梯形,可用两种方法,每一种把图形分割成为两个矩形.利用它们之间的面积关系,可以得到:a1b1+a2b2=( )
A.a1(b1-b2)+(a1+a2)b1
B.a2(b2-b1)+(a1+a2)b2
C.a1(b1-b2)+(a1+a2)b2
D.a2(b1-b2)+(a1+a2)b1
【答案】分析:这个图形的面积可以有两种算法,一种是上下把它分成两个矩形,一种是左右把它分成两个矩形.分别表示面积求解.
解答:解:这个图形的面积可以有两种算法:
一种是上下把它分成两个矩形,则它的面积是a1(b1-b2)+(a1+a2)b2;
一种是左右把它分成两个矩形.则它的面积就是a1b1+a2b2.所以a1b1+a2b2=a1(b1-b2)+(a1+a2)b2.
故选C.
点评:本题的关键是把这个图形进行分割,而且分割的方法有两种,且面积相等.
解答:解:这个图形的面积可以有两种算法:
一种是上下把它分成两个矩形,则它的面积是a1(b1-b2)+(a1+a2)b2;
一种是左右把它分成两个矩形.则它的面积就是a1b1+a2b2.所以a1b1+a2b2=a1(b1-b2)+(a1+a2)b2.
故选C.
点评:本题的关键是把这个图形进行分割,而且分割的方法有两种,且面积相等.

练习册系列答案
相关题目