Question

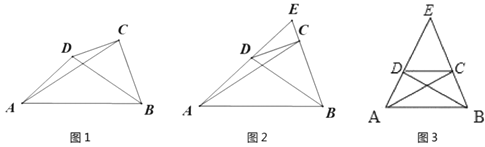
【题目】如图1，定义：在四边形中，若，则把四边形叫做互补四边形．

（1）如图2，分别延长互补四边形两边、交于点，求证：．

（2）如图3，在等腰中，，、分别为、上的点，四边形是互补四边形，，证明：．

Answer 1

【答案】（1）见解析；（2）见解析．

【解析】

（1）结合互补四边形的定义，利用三角形外角的性质可证，利用三角形内角和定理可证，由此可证；

（2）根据（1）的结论结合，可证，再根据等腰三角形的性质可证，再利用公共边AB可证明≌，根据全等三角形的性质和互补四边形的定义可证，再根据勾股定理可证．

解：（1）证明：如下图，

∵

∴，

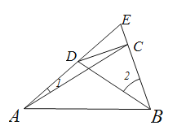
又∵,

∴，

∴;

（2）由（1）得，

又∵，

∴，

∵,

∴,

又∵AB=BA，

∴≌(ASA)，

∴，

又∵，

∴，

∴△ABD为直角三角形，．