题目内容
(1)如图1,AB为圆O的直径,弦CD⊥AB,垂足为点E,连结OC,若AB=10,CD=8,求AE的长.
(2)如图2,∠AOP=∠BOP=15°,PC∥OA,PD⊥OA,若PC=4,求PD的长度.
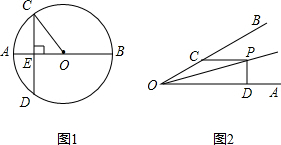
(2)如图2,∠AOP=∠BOP=15°,PC∥OA,PD⊥OA,若PC=4,求PD的长度.

分析:(1)根据垂径定理可以得到CE的长,在直角△OCE中,根据勾股定理即可求得.
(2)先过点P作PE⊥OB于E,根据两直线平行,内错角相等可得∠AOP=∠COP,然后利用三角形的一个外角等于与它不相邻的两个内角的和求出∠PCE=∠AOB=30°,再根据直角三角形30°角所对的直角边等于斜边的一半解答即可.
(2)先过点P作PE⊥OB于E,根据两直线平行,内错角相等可得∠AOP=∠COP,然后利用三角形的一个外角等于与它不相邻的两个内角的和求出∠PCE=∠AOB=30°,再根据直角三角形30°角所对的直角边等于斜边的一半解答即可.
解答: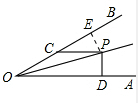 解:(1)∵AB为圆O的直径,弦CD⊥AB,垂足为点E.
解:(1)∵AB为圆O的直径,弦CD⊥AB,垂足为点E.
∴CE=
CD=4.
在直角△OCE中,OE=
=
=3.
则AE=OA-OE=5-3=2;
(2)如图,过点P作PE⊥OB于E,
∵PC∥OA,
∴∠AOP=∠COP,
∴∠PCE=∠BOP+∠COP=∠BOP+∠AOP=∠AOB=30°,
又∵PC=4,
∴PE=
PC=
×4=2,
∵∠AOP=∠BOP,PD⊥OA,
∴PD=PE=2.
 解:(1)∵AB为圆O的直径,弦CD⊥AB,垂足为点E.
解:(1)∵AB为圆O的直径,弦CD⊥AB,垂足为点E.∴CE=
| 1 |
| 2 |
在直角△OCE中,OE=
| OC2-CE2 |
| 52-42 |
则AE=OA-OE=5-3=2;
(2)如图,过点P作PE⊥OB于E,
∵PC∥OA,
∴∠AOP=∠COP,
∴∠PCE=∠BOP+∠COP=∠BOP+∠AOP=∠AOB=30°,
又∵PC=4,
∴PE=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠AOP=∠BOP,PD⊥OA,
∴PD=PE=2.
点评:此题考查了垂经定理和30°角的直角三角形,用到的知识点是垂经定理、勾股定理、直角三角形中0°角所对的直角边等于斜边的一半,关键是作辅助线构造出含30°的直角三角形.

练习册系列答案
相关题目
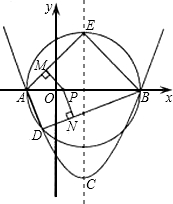 已知:抛物线y=ax2+bx+c(a≠0),顶点C(1,-3),与x轴交于A,B两点,A(-1,0).
已知:抛物线y=ax2+bx+c(a≠0),顶点C(1,-3),与x轴交于A,B两点,A(-1,0).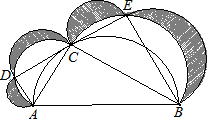 如图,以AB为直径作半圆与直角梯形ABED另一腰DE相切于C点,再分别以AC、BC、
如图,以AB为直径作半圆与直角梯形ABED另一腰DE相切于C点,再分别以AC、BC、 (2012•永安市质检)如图,以AB为直径的⊙O经过点C,D是AB延长线上一点,且DC=AC,∠CAB=30°.
(2012•永安市质检)如图,以AB为直径的⊙O经过点C,D是AB延长线上一点,且DC=AC,∠CAB=30°. 如图,以AB为直径的⊙O与直线CD相切于点E,且AC⊥CD,BD⊥CD,AC=8cm,BD=2cm,求四边形ACDB的面积.
如图,以AB为直径的⊙O与直线CD相切于点E,且AC⊥CD,BD⊥CD,AC=8cm,BD=2cm,求四边形ACDB的面积.