题目内容
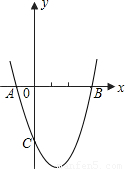
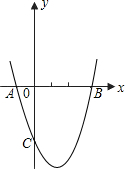 如图二次函数y=x2+bx+c的图象经过A(-1,0)和B(3,0)两点,且交y轴于点C.
如图二次函数y=x2+bx+c的图象经过A(-1,0)和B(3,0)两点,且交y轴于点C.(1)试确定b、c的值;
(2)过点C作CD∥x轴交抛物线于点D,点M为此抛物线的顶点,试确定△MCD的形状.
参考公式:顶点坐标(-
| b |
| 2a |
| 4ac-b2 |
| 4a |
分析:(1)把A和B两点的坐标代入函数解析式,就可以得到一个关于b,c的方程组,解方程组就可以求出b,c的值.
(2)根据抛物线的顶点坐标的公式代入就可以求出顶点坐标,在抛物线的解析式中,令x=0,解得C点的坐标;C点与D的纵坐标相同,把纵坐标的值代入函数解析式就可以得到D点的坐标,根据坐标就可以求出△CDM的三边的长度.从而判断三角形的形状.
(2)根据抛物线的顶点坐标的公式代入就可以求出顶点坐标,在抛物线的解析式中,令x=0,解得C点的坐标;C点与D的纵坐标相同,把纵坐标的值代入函数解析式就可以得到D点的坐标,根据坐标就可以求出△CDM的三边的长度.从而判断三角形的形状.
解答:解:(1)将A、B两点坐标代入解析式,有:
(1分)
解得:b=-2,c=-3(2分)
(2)在函数y=x2+bx+c中a=1,b=-2,c=-3,因而-
=1
=-4
∴抛物线的顶点M(1,-4)
在函数y=x2-2x-3中,令x=0,解得y=-3
∴C点的坐标是(0,-3),
把y=-3代入函数y=x2-2x-3,
解得x=2则D点的坐标是(2,-3),CD=2,CM=
=
同理DM=
∴△CDM是等腰直角三角形.
|
解得:b=-2,c=-3(2分)
(2)在函数y=x2+bx+c中a=1,b=-2,c=-3,因而-
| b |
| 2a |
| 4ac-b2 |
| 4a |
∴抛物线的顶点M(1,-4)
在函数y=x2-2x-3中,令x=0,解得y=-3
∴C点的坐标是(0,-3),
把y=-3代入函数y=x2-2x-3,
解得x=2则D点的坐标是(2,-3),CD=2,CM=
| (1-0)2+(-4+3)2 |
| 2 |
同理DM=
| 2 |
∴△CDM是等腰直角三角形.
点评:本题主要考查了待定系数法求函数解析式,利用公式法求函数的解析式,以及利用勾股定理的逆定理判断三角形是直角三角形.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
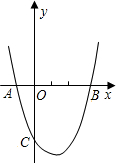 如图二次函数y=x2+bx+c的图象经过A(-1,0)和B(3,0)两点,且交y轴于点C.过点C作CD∥x轴交抛物线于点D,点M为此抛物线的顶点
如图二次函数y=x2+bx+c的图象经过A(-1,0)和B(3,0)两点,且交y轴于点C.过点C作CD∥x轴交抛物线于点D,点M为此抛物线的顶点 如图二次函数y=x2+bx+c的图象经过A(-1,0)和B(3,0)两点,且交y轴于点C.
如图二次函数y=x2+bx+c的图象经过A(-1,0)和B(3,0)两点,且交y轴于点C.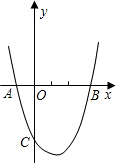 如图二次函数y=x2+bx+c的图象经过A(-1,0)和B(3,0)两点,且交y轴于点C.过点C作CD∥x轴交抛物线于点D,点M为此抛物线的顶点
如图二次函数y=x2+bx+c的图象经过A(-1,0)和B(3,0)两点,且交y轴于点C.过点C作CD∥x轴交抛物线于点D,点M为此抛物线的顶点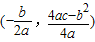 .
.