题目内容
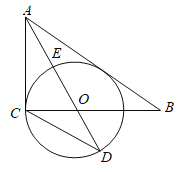
【题目】如图1,在直角△ABC中,∠ACB=90°,AO是△ABC的角平分线,以O为圆心,OC为半径作圆O
(1)求证:AB是⊙O的切线;
(2)已知AO交圆O于点E,延长AO交圆O于点D,tan∠D=![]() ,求
,求![]() 的值;
的值;
(3)如图2,在(2)条件下,若AB与⊙O的切点为点F,连接CF交AD于点G,设⊙O的半径为3,求CF的长.
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)由于题目没有说明直线AB与⊙O有交点,所以过点O作OF⊥AB于点F,然后证明OC=OF即可;
(2)连接CE,先求证∠ACE=∠ODC,然后可知△ACE∽△ADC,则![]() ,而tan∠D=
,而tan∠D=![]() ,即可求解;
,即可求解;
(3)连接CF交AD于点M,由(2)可知,AC2=AEAD,先求出AE,AC的长,则AO可求出,证△CMO∽△ACO,可得OC2=OMOA,求出OM,CM,则CF=2CM可求解.
(1)证明:如图,过点O作OF⊥AB于点F
,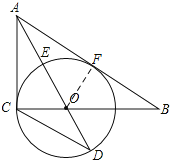
∵AO平分∠CAB,
OC⊥AC,OF⊥AB,
∴OC=OF,
∴AB是⊙O的切线;
(2)解:如图,连接CE,
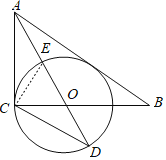
∵ED是⊙O的直径,
∴∠ECD=90°,
∴∠ECO+∠OCD=90°,
∵∠ACB=90°,
∴∠ACE+∠ECO=90°,
∴∠ACE=∠OCD,
∵OC=OD,
∴∠OCD=∠ODC,
∴∠ACE=∠ODC,
∵∠CAE=∠CAE,
∴△ACE∽△ADC,
∴![]() ,
,
∵tan![]() ,
,
∴![]() ;
;
(3)由(2)可知:![]() ,
,
∴设AE=x,AC=2x,
∵△ACE∽△ADC,
∴![]() ,
,
∴AC2=AEAD,
∴(2x)2=x(x+6),
解得:x=2或x=0(不合题意,舍去),
∴AE=2,AC=4,
∴AO=AE+OE=2+3=5,
如图,连接CF交AD于点M
,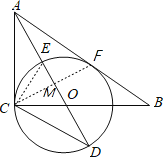
∵AC,AF是⊙O的切线,
∴AC=AF,∠CAO=∠OAF,
∴CF⊥AO,
∴∠ACO=∠CMO=90°,
∵∠COM=∠AOC,
∴△CMO∽△ACO,
∴![]() ,
,
∴OC2=OMOA,
∴OM=![]() ,
,
∴CM=![]() =
=![]() ,
,
∴![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】商场里某产品每月销售量y(只)与销售单价x(元)满足一次函数关系,经调查部分数据如表:(已知每只进价为10元,每只利润=销售单价-进价)
销售单价x(元) | 21 | 23 | 25 | … |
月销售额y(只) | 29 | 27 | 25 | … |
(1)求出y与x之间的函数表达式;
(2)这产品每月的总利润为w元,求w关于x的函数表达式,并指出销售单价为多少元时利润最大,最大利润是多少元?
(3)由于该产品市场需求量较大,进价在原有基础上提高了a元(a<10),但每月销售量与销售价仍满足上述一次函数关系,此时,随着销售量的增大,所得的最大利润比(2)中的最大利润减少了144元,求a的值.