题目内容
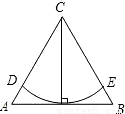
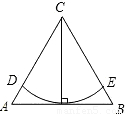
 如图,在边长为20cm的等边三角形ABC纸片中,以顶点C为圆心,以此三角形的高为半径画弧分别交AC、BC于点D、E,则扇形CDE所围的圆锥(不计接缝)的底圆半径为( )
如图,在边长为20cm的等边三角形ABC纸片中,以顶点C为圆心,以此三角形的高为半径画弧分别交AC、BC于点D、E,则扇形CDE所围的圆锥(不计接缝)的底圆半径为( )A、
| ||||
B、
| ||||
C、5
| ||||
D、10
|
分析:根据等边三角形的性质,利用弧长的计算方法,采用排除法求解即可.
解答:解:扇形CDE的圆心角是60°,半径是20•sin60°=10
,则弧长是
=
cm,圆锥的底面周长等于侧面展开图的扇形弧长,因而圆锥的底面周长是
cm,设圆锥的底面半径是r,则得到2πr=
,解得:r=
故选A.
| 3 |
60π•10
| ||
| 180 |
10
| ||
| 3 |
10
| ||
| 3 |
10
| ||
| 3 |
5
| ||
| 3 |
故选A.
点评:本题综合考查有关扇形和圆锥的相关计算.解题思路:解决此类问题时要紧紧抓住两者之间的两个对应关系:
(1)圆锥的母线长等于侧面展开图的扇形半径;
(2)圆锥的底面周长等于侧面展开图的扇形弧长.正确对这两个关系的记忆是解题的关键.
(1)圆锥的母线长等于侧面展开图的扇形半径;
(2)圆锥的底面周长等于侧面展开图的扇形弧长.正确对这两个关系的记忆是解题的关键.

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案
相关题目
如图,在边长为20cm的等边三角形ABC纸片中,以顶点C为圆心,以此三角形的高为半径画弧分别交AC、BC于点D、E,则扇形CDE所围的圆锥(不计接缝)的底圆半径为( )
A.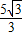 cm
cm
B.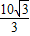 cm
cm
C.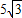 cm
cm
D.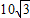 cm
cm

A.
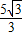 cm
cmB.
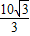 cm
cmC.
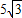 cm
cmD.
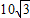 cm
cm
如图,在边长为20cm的等边三角形ABC纸片中,以顶点C为圆心,以此三角形的高为半径画弧分别交AC、BC于点D、E,则扇形CDE所围的圆锥(不计接缝)的底圆半径为( )
A. cm
cm
B.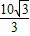 cm
cm
C.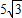 cm
cm
D.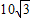 cm
cm

A.
 cm
cmB.
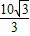 cm
cmC.
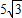 cm
cmD.
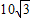 cm
cm
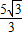 cm
cm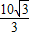 cm
cm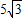 cm
cm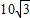 cm
cm
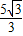 cm
cm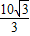 cm
cm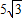 cm
cm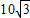 cm
cm