题目内容
已知二次函数y=ax2+bx+c(a≠0),给出下列四个判断:(1)a>0;(2)2a+b=0;(3)b2-4ac>0;(4)a+b+c<0;以其中三个判断为条件,余下一个判断作结论,其中真命题的个数有( )
| A.1 个 | B.2 个 | C.3 个 | D.4 个 |
(1)∵①a>0,
∴开口向上,
∵②2a+b=0,
∴对称轴为x=1,
∵③b2-4ac>0,
∴顶点在第四象限,
∴④a+b+c<0正确;
(2)∵①a>0,
∴开口向上,
∵②2a+b=0,
∴对称轴为x=1,
∵④a+b+c<0,
∴顶点在第四象限,
∴③b2-4ac>0正确;
(3)∵①a>0,
∴开口向上,
∵③b2-4ac>0,④a+b+c<0,
∴顶点在第三、四象限,
∴②2a+b=0错误;
(4)∵②2a+b=0,
∴对称轴为x=1,
∵③b2-4ac>0,④a+b+c<0,
∴顶点在第四象限,
∴与x轴有两个交点,
∴①a>0正确.
故选C.
∴开口向上,
∵②2a+b=0,
∴对称轴为x=1,
∵③b2-4ac>0,
∴顶点在第四象限,
∴④a+b+c<0正确;
(2)∵①a>0,
∴开口向上,
∵②2a+b=0,
∴对称轴为x=1,
∵④a+b+c<0,
∴顶点在第四象限,
∴③b2-4ac>0正确;
(3)∵①a>0,
∴开口向上,
∵③b2-4ac>0,④a+b+c<0,
∴顶点在第三、四象限,
∴②2a+b=0错误;
(4)∵②2a+b=0,
∴对称轴为x=1,
∵③b2-4ac>0,④a+b+c<0,
∴顶点在第四象限,
∴与x轴有两个交点,
∴①a>0正确.
故选C.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知二次函数y=ax+bx+c(a≠0,a,b,c为常数),对称轴为直线x=1,它的部分自变量与函数值y的对应值如下表,写出方程ax2+bx+c=0的一个正数解的近似值________(精确到0.1).
| x | -0.1 | -0.2 | -0.3 | -0.4 |
| y=ax2+bx+c | -0.58 | -0.12 | 0.38 | 0.92 |
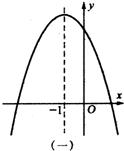 21、已知二次函数y=a(x+1)2+c的图象如图所示,则函数y=ax+c的图象只可能是( )
21、已知二次函数y=a(x+1)2+c的图象如图所示,则函数y=ax+c的图象只可能是( )
