题目内容
已知抛物线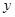 =
=![]() +
+![]() +
+![]() -4.
-4.
(1)当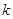 =2时,求出此抛物线的顶点坐标;
=2时,求出此抛物线的顶点坐标;
(2)求证:无论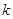 为什么实数,抛物线都与
为什么实数,抛物线都与![]() 轴有交点,且经过
轴有交点,且经过![]() 轴上的一定点;
轴上的一定点;
(3)已知抛物线与![]() 轴交于A(
轴交于A(![]() 1,0)、B(
1,0)、B(![]() 2,0)两点(A在B的左边),|
2,0)两点(A在B的左边),|![]() 1|<|
1|<|![]() 2|,与
2|,与![]() 轴交于C点,且S△ABC=15.问:过A,B,C三点的圆与该抛物线是否有第四个交点?试说明理由.如果有,求出其坐标.
轴交于C点,且S△ABC=15.问:过A,B,C三点的圆与该抛物线是否有第四个交点?试说明理由.如果有,求出其坐标.
(1)(-1,-1)(2)当≥4时,当
<4时(3)有第四个交点,(1,-6)
解析:解:(1)当=2时,抛物线为
=
+
,…………………………1分
配方:=
+
=
+
+1-1
得=
-1,
∴顶点坐标为(-1,-1);………………………………………………3分
(也可由顶点公式求得)
(2)令=0,有
+
+
-4=0,………………………………4分
此一元二次方程根的判别式
⊿=-4·(
-4)=
-
+16=
,…………………5分
∵无论为什么实数,
≥0,
方程+
+
-4=0都有解,…………………………………………6分
即抛物线总与轴有交点.
由求根公式得=
,………………………………………………7分
当![]() ≥4时,
≥4时,=
,
1=
=-2,
2=
=-
+2;
当![]() <4时,
<4时,=
,
1=
=-
+2,
2=
=-2.
即抛物线与轴的交点分别为(-2,0)和(-
+2,0),
而点(-2,0)是轴上的定点;…………………………………………8分
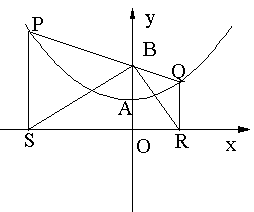
(3)过A,B,C三点的圆与该抛物线有第四个交点.…………………9分
设此点为D.∵|1|<|
2|,C点在y轴上,
由抛物线的对称,可知点C不是抛物线的顶点.……………………………10分
由于圆和抛物线都是轴对称图形,
过A、B、C三点的圆与抛物线组成一个轴对称图形.……………………11分
∵轴上的两点A、B关于抛物线对称轴对称,
∴过A、B、C三点的圆与抛物线的第四个
交点D应与C点关于抛物线对称轴对称.……………………………………12分
由抛物线与轴的交点分别为(-2,0)和(-
+2,0):
当-2<-+2,即
<4时,…………………………13分
A点坐标为(-2,0),B为(-+2,0).
即1=-2,
2=-
+2.
由|1|<|
2|得-
+2>2,解得
<0.
根据S△ABC=15,得AB·OC=15.
AB=-+2-(-2)=4-
,
OC=|2-4|=4-2
,
∴(4-
)(4-2
)=15,
化简整理得=0,
解得=7(舍去)或
=-1.
此时抛物线解析式为=
,
其对称轴为=
,C点坐标为(0,-6),
它关于=
的对称点D坐标为(1,-6);………………………………14分
当-2>-+2,由A点在B点左边,
知A点坐标为(-+2,0),B为(-2,0).
即1=-
+2,
2=-2.
但此时|1|>|
2|,这与已知条件|
1|<|
2|不相符,
∴不存在此种情况.
故第四个交点的坐标为(1,-6).
(如图6)
(1)把![]() =2代入抛物线,通过配方可求得此抛物线的顶点坐标
=2代入抛物线,通过配方可求得此抛物线的顶点坐标
(2)令y=0,解方程![]() +
+![]() +
+![]() -4,即可求出抛物线与x轴两交点的横坐标,定点为与k值无关的点;
-4,即可求出抛物线与x轴两交点的横坐标,定点为与k值无关的点;
(3)过A、B、C三点的圆与抛物线有第四个交点D,根据A、B、C三点坐标,讨论k的范围,表示△ABC的面积,列方程求k,再根据对称性求D点坐标

 轻松暑假总复习系列答案
轻松暑假总复习系列答案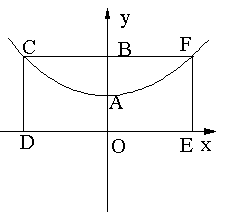
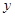 =
=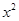 +
+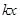 +
+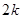 -4.
-4.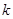 =2时,求出此抛物线的顶点坐标;
=2时,求出此抛物线的顶点坐标;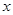 轴有交点,且经过
轴有交点,且经过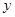 =
=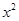 +
+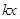 +
+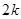 -4.
-4.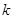 =2时,求出此抛物线的顶点坐标;
=2时,求出此抛物线的顶点坐标; 轴有交点,且经过
轴有交点,且经过