题目内容
【题目】将一副三角板拼成如图所示的图形,过点C作CF∥AB交DE于点F. 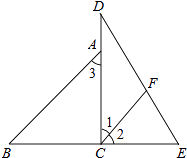
(1)求证:CF平分∠DCE;
(2)求∠DFC的度数.
【答案】
(1)证明:∵△ABC是等腰直角三角形,
∴∠3=∠B=45°,
∵CF∥AB,
∴∠3=∠1=45°,
∵∠DCB=90°,
∴∠2=∠DCB﹣∠1=90°﹣45°=45°,
∴∠1=∠2,
∴CF平分∠DCE
(2)在△EFC中,∠E=60°,
∴∠DFC=∠E+∠2=60°+45°=105°
【解析】(1)由已知的一副三角板可知:△ABC是等腰直角三角形,则∠3=∠B=45°,由平行线所截得内错角相等得:∠1=∠3=45°,所以∠2=45°,从而得出结论;(2)根据外角定理可得:∠DFC=∠E+∠2.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】有甲、乙两个社区乐团,决定向某服装厂购买同样的演出服.如表是服装厂给出的演出服装的价格表:
购买服装的套数 | 1~39套(含39套) | 40~69套(含69套) | 70套及以上 |
每套服装的价格 | 80元 | 70元 | 60元 |
经调查:两个乐团共85人(甲乐团人数不少于46人,不大于70人),如果分别各自购买演出服,两个乐团共需花费6300元.
(1)如果甲、乙两个乐团联合起来购买服装,那么比各自购买服装最多可以节省多少元?
(2)甲、乙两个乐团各有多少名成员?
(3)现从甲乐团抽调a人,从乙乐团抽调b人(要求从每个乐团抽调的人数不少于5人),去儿童福利院献爱心演出.并在演出后每位乐团成员向儿童们进行“心连心活动”;甲乐团每位成员负责5位小朋友,乙乐团每位成员负责3位小朋友.这样恰好使得福利院75位小朋友全部得到“心连心活动”的温暖.请写出所有的抽调方案.并说明理由。