题目内容
如图，将矩形纸片ABCD(AD>DC)的一角沿着过点D的直线折叠，使点A
与BC边上的点E重合，折痕交AB于点F.若BE:EC=m:n，则AF:FB= ▼.
与BC边上的点E重合，折痕交AB于点F.若BE:EC=m:n，则AF:FB= ▼.
①根据题意，BC=3=AD=DE，根据三角函数定义易求sin∠EDC；
②AF：FB=EF：FB．证明△BEF∽△CDE可得EF：FB=DE：EC，由BE：EC=m：n可求解．
解：∵BE=1，EC=2，∴BC=3．
∵BC=AD=DE，∴DE=3．
sin∠EDC=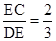
；
∵∠DEF=90°，∴∠BEF+∠CED=90°．
又∠BEF+∠BFE=90°，
∴∠BFE=∠CED．又∠B=∠C，
∴△BEF∽△CDE．
∴EF：FB=DE：EC．
∵BE：EC=m：n，
∴可设BE=mk，EC=nk，则DE=（m+n）k．
∴EF：FB=DE：EC=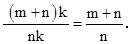
∵AF=EF，
∴AF：FB=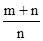
②AF：FB=EF：FB．证明△BEF∽△CDE可得EF：FB=DE：EC，由BE：EC=m：n可求解．
解：∵BE=1，EC=2，∴BC=3．
∵BC=AD=DE，∴DE=3．
sin∠EDC=
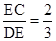；∵∠DEF=90°，∴∠BEF+∠CED=90°．
又∠BEF+∠BFE=90°，
∴∠BFE=∠CED．又∠B=∠C，
∴△BEF∽△CDE．
∴EF：FB=DE：EC．
∵BE：EC=m：n，
∴可设BE=mk，EC=nk，则DE=（m+n）k．
∴EF：FB=DE：EC=
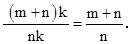
∵AF=EF，
∴AF：FB=
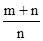
练习册系列答案
相关题目
E的度数；
,对角线AC、BD相交于点0，将直线AC绕点0顺时针旋转，分别交BC、AD于点E、F.
