题目内容
如图1,△ABC是直角三角形,AB为斜边,sin∠BAC= ,现要将它放置在如图2的平面直
,现要将它放置在如图2的平面直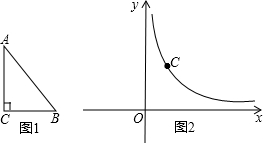 角坐标系中,使斜边AB落在x轴上,直角顶点C(1,3)落在反比例函数y=
角坐标系中,使斜边AB落在x轴上,直角顶点C(1,3)落在反比例函数y= (x>0)的图象上.
(x>0)的图象上.
(1)求k的值和边AC的长;
(2)求点B的坐标.
 解:(1)作CD⊥x轴于D.则CD=3.
解:(1)作CD⊥x轴于D.则CD=3.把(1,3)代入y=
 得:3=k,则k=3,
得:3=k,则k=3,∵sin∠BAC=
 =
= ,
,∴AC=5;
(2)直角△ACD中,AD=
 =4,
=4,则BD=AB-AD=1,
因为C的坐标是(1,3),则OD=1,
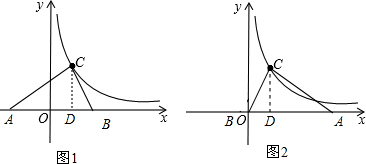
当AB的位置如图1时,OB=OD+BD=1+1=2,则B的坐标是(2,0);
当AB的位置如图2,时:OB=BD-OD=0,即B和O重合,则B的坐标是(0,0).
故B的坐标是(2,0)或(0,0).
分析:(1)把C的坐标代入反比例函数的解析式即可求得k的值,然后利用三角函数即可求得AC的长;
(2)在直角△ACD中,利用勾股定理即可求得AD的长,然后分两种情况求得OB的长度,即可得到B的坐标.
点评:本题考查了待定系数法求函数的解析式,以及勾股定理,正确求得AD的长度是关键.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
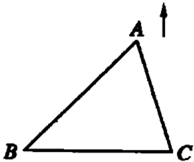 20、如图,在△ABC中,BC边不动,点A是一个动点.当点A竖直向上运动,∠A越来越小,∠B、∠C越来越大.若∠A减少α度,∠B增加β度,∠C增加γ度,请写出α、β、γ三者之间的等量关系,并说明你是如何得到的.
20、如图,在△ABC中,BC边不动,点A是一个动点.当点A竖直向上运动,∠A越来越小,∠B、∠C越来越大.若∠A减少α度,∠B增加β度,∠C增加γ度,请写出α、β、γ三者之间的等量关系,并说明你是如何得到的. 30、如图,在△ABC中,AB=AC,D是BC的中点,连接AD.DE⊥AB,DF⊥AC,E,F是垂足.图中共有多少对全等三角形?请直接用“≌”符号把它们分别表示出来.(不要求证明)
30、如图,在△ABC中,AB=AC,D是BC的中点,连接AD.DE⊥AB,DF⊥AC,E,F是垂足.图中共有多少对全等三角形?请直接用“≌”符号把它们分别表示出来.(不要求证明)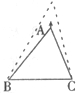 14、如图,在△ABC中,BC边不动,点A竖直向上运动,∠A越来越小,∠B,∠C越来越大.若∠A减小x°,∠B增加y°,∠C增加z°,则x,y,z之间的关系是( )
14、如图,在△ABC中,BC边不动,点A竖直向上运动,∠A越来越小,∠B,∠C越来越大.若∠A减小x°,∠B增加y°,∠C增加z°,则x,y,z之间的关系是( ) 学习过三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.类似的,也可以在等腰三角形中建立边角之间的联系,我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图,在△ABC中,AB=AC,顶角A的正对记作sadA,这时sad A=
学习过三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.类似的,也可以在等腰三角形中建立边角之间的联系,我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图,在△ABC中,AB=AC,顶角A的正对记作sadA,这时sad A=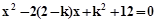 有实数根α、β.求实数k的取值范围;设
有实数根α、β.求实数k的取值范围;设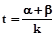 ,求t的最小值.
,求t的最小值.