题目内容
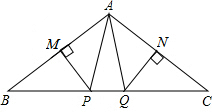 如图所示,∠BAC=100°,若MP、NQ分别垂直平分AB、AC.若BC=10cm,则△APQ的周长为________,∠PAQ=________.
如图所示,∠BAC=100°,若MP、NQ分别垂直平分AB、AC.若BC=10cm,则△APQ的周长为________,∠PAQ=________.
10cm 20°
分析:由MP、NQ分别垂直平分AB、AC,根据线段垂直平分线的性质,可得AP=BP,AQ=CQ,继而求得△APQ的周长=BC;
由三角形内角和定理,可求得∠B+∠C,又由等腰三角形的性质,可求得∠BAP+∠CAQ,继而求得答案.
解答:∵MP、NQ分别垂直平分AB、AC,
∴AP=BP,AQ=CQ,
∵BC=10cm,
∴△APQ的周长为:AP+PQ+AQ=BP+PQ+CQ=BC=10(cm);
∵∠BAC=100°,
∴∠B+∠C=80°,
∵AP=BP,AQ=CQ,
∴∠BAP=∠B,∠CAQ=∠C,
∴∠BAP+∠CAQ=∠B+∠C=80°,
∴∠PAQ=∠BAC-(∠BAP+∠CAQ)=20°.
故答案为:10cm,20°.
点评:此题考查了线段垂直平分线的性质以及等腰三角形的性质.此题难度不大,注意掌握数形结合思想的应用.
分析:由MP、NQ分别垂直平分AB、AC,根据线段垂直平分线的性质,可得AP=BP,AQ=CQ,继而求得△APQ的周长=BC;
由三角形内角和定理,可求得∠B+∠C,又由等腰三角形的性质,可求得∠BAP+∠CAQ,继而求得答案.
解答:∵MP、NQ分别垂直平分AB、AC,
∴AP=BP,AQ=CQ,
∵BC=10cm,
∴△APQ的周长为:AP+PQ+AQ=BP+PQ+CQ=BC=10(cm);
∵∠BAC=100°,
∴∠B+∠C=80°,
∵AP=BP,AQ=CQ,
∴∠BAP=∠B,∠CAQ=∠C,
∴∠BAP+∠CAQ=∠B+∠C=80°,
∴∠PAQ=∠BAC-(∠BAP+∠CAQ)=20°.
故答案为:10cm,20°.
点评:此题考查了线段垂直平分线的性质以及等腰三角形的性质.此题难度不大,注意掌握数形结合思想的应用.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
 如图所示,∠BAC=90°,O为AB上一点,以O为圆心,
如图所示,∠BAC=90°,O为AB上一点,以O为圆心,| 1 |
| 2 |
| A、30° | B、60° |
| C、60°或120° | D、120° |
 5、如图所示,∠BAC=90°,AB=AC,过点A任意作一直线DE,且作CE⊥ED,BD⊥ED,经测量CE=2cm,BD=4cm,则DE的长为( )
5、如图所示,∠BAC=90°,AB=AC,过点A任意作一直线DE,且作CE⊥ED,BD⊥ED,经测量CE=2cm,BD=4cm,则DE的长为( )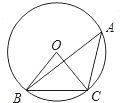 如图所示,∠BAC是⊙O的圆周角,则∠BAC+∠OCB=
如图所示,∠BAC是⊙O的圆周角,则∠BAC+∠OCB= 19、如图所示,∠BAC=∠ABD,AC=BD,点O是AD、BC的交点,点E是AB的中点.
19、如图所示,∠BAC=∠ABD,AC=BD,点O是AD、BC的交点,点E是AB的中点.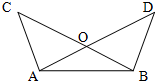 18、如图所示,∠BAC=∠ABD,AC=BD,点O是AD、BC的交点,
18、如图所示,∠BAC=∠ABD,AC=BD,点O是AD、BC的交点,