Question

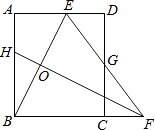
【题目】如图，已知正方形ABCD的边长为4，对称中心为点P，点F为BC边上一个动点，点E在AB边上，且满足条件∠EPF=45°，图中两块阴影部分图形关于直线AC成轴对称，设它们的面积和为S1 ．

（1）求证：∠APE=∠CFP；
（2）设四边形CMPF的面积为S2 ， CF=x， ．
①求y关于x的函数解析式和自变量x的取值范围，并求出y的最大值；
②当图中两块阴影部分图形关于点P成中心对称时，求y的值．

Answer 1

【答案】
（1）

证明：∵∠EPF=45°，

∴∠APE+∠FPC=180°﹣45°=135°；

而在△PFC中，由于PC为正方形ABCD的对角线，则∠PCF=45°，

则∠CFP+∠FPC=180°﹣45°=135°，

∴∠APE=∠CFP

（2）

解：①∵∠APE=∠CFP，且∠FCP=∠PAE=45°，

∴△APE∽△CFP，则 ．

而在正方形ABCD中，AC为对角线，则AC= AB= ，

又∵P为对称中心，则AP=CP= ，

∴AE= = = ．

如图，过点P作PH⊥AB于点H，PG⊥BC于点G，

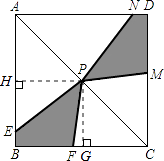
P为AC中点，则PH∥BC，且PH= BC=2，同理PG=2．

S△APE= = ×2× = ，

∵阴影部分关于直线AC轴对称，

∴△APE与△APN也关于直线AC对称，

则S四边形AEPN=2S△APE= ；

而S2=2S△PFC=2× =2x，

∴S1=S正方形ABCD﹣S四边形AEPN﹣S2=16﹣ ﹣2x，

∴y= = = + ﹣1．

∵E在AB上运动，F在BC上运动，且∠EPF=45°，

∴2≤x≤4．

令 =a，则y=﹣8a2+8a﹣1，当a= = ，即x=2时，y取得最大值．

而x=2在x的取值范围内，代入x=2，则y最大=4﹣2﹣1=1．

∴y关于x的函数解析式为：y= + ﹣1（2≤x≤4），y的最大值为1．

②图中两块阴影部分图形关于点P成中心对称，

而此两块图形也关于直线AC成轴对称，则阴影部分图形自身关于直线BD对称，

则EB=BF，即AE=FC，

∴ =x，解得x= ，

代入x= ，得y= ﹣2．

【解析】（1）利用正方形与三角形的相关角之间的关系可以证明结论；
（2）本问关键是求出y与x之间的函数解析式．①首先分别用x表示出S1与S2 ， 然后计算出y与x的函数解析式．这是一个二次函数，求出其最大值；②注意中心对称、轴对称的几何性质．
【考点精析】本题主要考查了相似三角形的性质的相关知识点，需要掌握对应角相等，对应边成比例的两个三角形叫做相似三角形才能正确解答此题．