题目内容
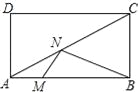
【题目】如图，在矩形ABCD中，AB=4，AD=2，点M是AB上一动点，点N是对角线AC上一动点，则MN+BN的最小值为______.
【答案】
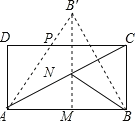
【解析】试题分析：作点B关于AC的对称点B′，过点B′作B′M⊥AB于M，交AC于N，
连接AB′交DC于P，连接BN， ∵四边形ABCD是矩形， ∴DC∥AB，
∴∠BAC=∠PCA， ∵点B关于AC的对称点是B′， ∴∠PAC=∠BAC，
∴∠PAC=∠PCA， ∴PA=PC． 令PA=x，则PC=x，PD=8-x．
在Rt△ADP中， 
， ∴x=
，
∵cos∠B′AM=cos∠APD， ∴AM：AB′=DP：AP， ∴AM：4=1.5：2.5，
∴AM=
，∴B′M=AB′2-AM2=，
∴MN+BN的最小值=．
练习册系列答案
相关题目
