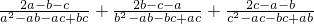题目内容
化简计算（式中a，b，c两两不相等）：| 2a-b-c |
| a2-ab-ac+bc |
| 2b-c-a |
| b2-ab-bc+ac |
| 2c-a-b |
| c2-ac-bc+ab |
分析：本题关键是明确分式
的变形，其他两项是类似的，对于这个分式，显然分母可以分解因式为（a-b）（a-c），而分子又恰好凑成（a-b）+（a-c），可以将一个分式分为两个分式的和，寻找抵消规律．
| 2a-b-c |
| a2-ab-ac+bc |
解答：解：原式=
+
+
=
+
+
+
+
+
=0．
| (a-b)+(a-c) |
| (a-b)(a-c) |
| (b-c)+(b-a) |
| (b-c)(b-a) |
| (c-a)+(c-b) |
| (c-a)(c-b) |
=
| 1 |
| a-c |
| 1 |
| a-b |
| 1 |
| b-a |
| 1 |
| b-c |
| 1 |
| c-b |
| 1 |
| c-a |
点评：说明本例也是采取“拆项相消”法，所不同的是本题利用了
=
+
的变形技巧．
| A+B |
| AB |
| 1 |
| A |
| 1 |
| B |
练习册系列答案
优生乐园系列答案
相关题目
