题目内容
已知M、N两点关于y轴对称,且点M在反比例函数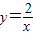 的图象上,点N在直线y=x+4上,设点M的坐标为(a,b),则二次函数y=-abx2+(a+b)x有( )
的图象上,点N在直线y=x+4上,设点M的坐标为(a,b),则二次函数y=-abx2+(a+b)x有( )A.最小值为2
B.最大值为2
C.最小值为-2
D.最大值为-2
【答案】分析:先用待定系数法求出二次函数的解析式,再根据二次函数图象上点的坐标特征求出其最值即可.
解答:解:∵M,N两点关于y轴对称,
∴设点M的坐标为(a,b),则N点的坐标为(-a,b),
又∵点M在反比例函数 的图象上,点N在一次函数y=x+4的图象上,
的图象上,点N在一次函数y=x+4的图象上,
∴ ,整理得
,整理得 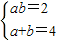 ,
,
故二次函数y=-abx2+(a+b)x为y=-2x2+4x,
∴二次项系数为-2<0,故函数有最大值,最大值为y=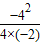 =2.
=2.
故选B.
点评:本题考查的是二次函数的最值.求二次函数的最大(小)值有三种方法,第一种可由图象直接得出,第二种是配方法,第三种是公式法.本题是利用公式法求得的最值.
解答:解:∵M,N两点关于y轴对称,
∴设点M的坐标为(a,b),则N点的坐标为(-a,b),
又∵点M在反比例函数
 的图象上,点N在一次函数y=x+4的图象上,
的图象上,点N在一次函数y=x+4的图象上,∴
 ,整理得
,整理得 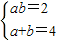 ,
,故二次函数y=-abx2+(a+b)x为y=-2x2+4x,
∴二次项系数为-2<0,故函数有最大值,最大值为y=
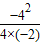 =2.
=2.故选B.
点评:本题考查的是二次函数的最值.求二次函数的最大(小)值有三种方法,第一种可由图象直接得出,第二种是配方法,第三种是公式法.本题是利用公式法求得的最值.

练习册系列答案
相关题目
已知M,N两点关于y轴对称,且点M在反比例函数y=
的图象上,点N在一次函数y=x+3的图象上,设点M的坐标为(a,b),则二次函数y=abx2+(a+b)x( )
| 1 |
| 2x |
A、有最小值,且最小值是
| ||
B、有最大值,且最大值是-
| ||
C、有最大值,且最大值是
| ||
D、有最小值,且最小值是-
|
已知M、N两点关于y轴对称,且点M在反比例函数y=
的图象上,点N在直线y=x+4上,设点M的坐标为(a,b),则二次函数y=-abx2+(a+b)x有( )
| 2 |
| x |
| A、最小值为2 |
| B、最大值为2 |
| C、最小值为-2 |
| D、最大值为-2 |