题目内容
 24、已知,如图,在正方形ABCD中,点E、F分别在AB上和AD的延长线上,且BE=DF,连接EF,G为EF的中点.
24、已知,如图,在正方形ABCD中,点E、F分别在AB上和AD的延长线上,且BE=DF,连接EF,G为EF的中点.求证:(1)CE=CF;(2)DG垂直平分AC.
分析:(1)利用三角形的全等,证明△CEB≌△CFD,即可解决;
(2)连接AG,CG,利用直角三角形斜边上的中线等于斜边的一半,得出AG=GE=GF,再证明∠ECF=90°,即可得出CG=GE=GF,结论得证.
(2)连接AG,CG,利用直角三角形斜边上的中线等于斜边的一半,得出AG=GE=GF,再证明∠ECF=90°,即可得出CG=GE=GF,结论得证.
解答: (1)证明:
(1)证明:
∵BE=DF,
BC=CD,
∠EBC=∠CDF,
∴△CEB≌△CFD,
∴CE=CF;
(2)证明
连接AG,CG
在Rt△EAF中,
∵G是斜边EF的中点,
∴AG=GE=GF,
又∵△EBC≌△FDC
∴∠ECB=∠FCD,∠BCD=90°,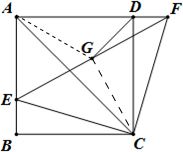
∴∠ECF=90°,
∴同理:CG=GE=GF,即GC=GA,
∴G点在AC的垂直平分线上,
又∵DA=DC,
∴D点也在AC的垂直平分线上,
∴DG垂直平分AC.
 (1)证明:
(1)证明:∵BE=DF,
BC=CD,
∠EBC=∠CDF,
∴△CEB≌△CFD,
∴CE=CF;
(2)证明
连接AG,CG
在Rt△EAF中,
∵G是斜边EF的中点,
∴AG=GE=GF,
又∵△EBC≌△FDC
∴∠ECB=∠FCD,∠BCD=90°,

∴∠ECF=90°,
∴同理:CG=GE=GF,即GC=GA,
∴G点在AC的垂直平分线上,
又∵DA=DC,
∴D点也在AC的垂直平分线上,
∴DG垂直平分AC.
点评:此题主要考查了正方形的性质以及直角三角形斜边上的中线等于斜边的一半等知识,分别得出AG=GE=GF,CG=GE=GF,是解决问题的关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
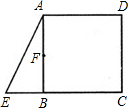 已知:如图,在正方形ABCD中,E是CB延长线上一点,EB=
已知:如图,在正方形ABCD中,E是CB延长线上一点,EB=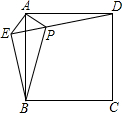 已知:如图,在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P.若AE=AP=1,PB=
已知:如图,在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P.若AE=AP=1,PB=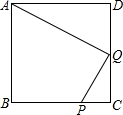 已知:如图,在正方形ABCD中,P是BC上的点,且BP=3PC,Q是CD的中点.△ADQ与△QCP是否相似?
已知:如图,在正方形ABCD中,P是BC上的点,且BP=3PC,Q是CD的中点.△ADQ与△QCP是否相似?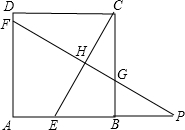 、CE、CB于点F、H、G,交AB的延长线于点P.
、CE、CB于点F、H、G,交AB的延长线于点P. 已知:如图,在正方形ABCD中,E、F分别是AD、CD的中点.
已知:如图,在正方形ABCD中,E、F分别是AD、CD的中点.